题目内容
2.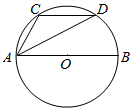 如图,AB是⊙O的直径,点C,D是半圆弧AB的三等分点,若$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,则$\overrightarrow{AD}$=$\frac{1}{2}$$\overrightarrow{a}$+$\overrightarrow{b}$.(用a,b表示)
如图,AB是⊙O的直径,点C,D是半圆弧AB的三等分点,若$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,则$\overrightarrow{AD}$=$\frac{1}{2}$$\overrightarrow{a}$+$\overrightarrow{b}$.(用a,b表示)
分析 连结CD、OD,由圆的性质与等腰三角形的性质,证出CD∥AB且AC∥DO,得到四边形ACDO为平行四边形,再根据题设条件即可得到用表示向量的式子.
解答 解:如图示: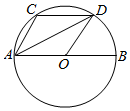
连结CD、OD,
∵点C、D是半圆弧AB的两个三等分点,
∴$\widehat{AC}$=$\widehat{BD}$,可得CD∥AB,∠CAD=∠DAB=$\frac{1}{3}$×90°=30°,
∵OA=OD,
∴∠ADO=∠DAO=30°,
由此可得∠CAD=∠DAO=30°,
∴AC∥DO.
∴四边形ACDO为平行四边形,
∴$\overrightarrow{AD}$=$\overrightarrow{AO}$+$\overrightarrow{AC}$=$\frac{1}{2}$$\overrightarrow{AB}$+$\overrightarrow{AC}$=$\frac{1}{2}$$\overrightarrow{a}$+$\overrightarrow{b}$,
故答案为:$\frac{1}{2}$$\overrightarrow{a}$+$\overrightarrow{b}$.
点评 本题给出半圆弧的三等分点,求向量的线性表示式.着重考查了圆周角定理、平行四边形的判定与向量的线性运算等知识,属于中档题.

练习册系列答案
相关题目
12.某农机租赁公司共有50台收割机,其中甲型20台,乙型30台,现将这50台联合收割机派往 A,B两地区收割水稻,其中30台派往 A地区,20台派往 B地区,两地区与该农机公司商定的每天租赁价格如表:
(1)设派往 A地区x台乙型联合收割机,租赁公司这50台联合收割机一天获得的租金为y元,求y关于x的函数关系式;
(2)若使农机租赁公司这50台收割机一天所获租金不低于79600元,试写出满足条件的所有分派方案;
(3)农机租赁公司拟出一个分派方案,使该公司50台收割机每天获得租金最高,并说明理由.
| 每台甲型收割机的租金 | 每台乙型收割机的租金 | |
| A地区 | 1800元 | 1600元 |
| B地区 | 1600元 | 1200元 |
(2)若使农机租赁公司这50台收割机一天所获租金不低于79600元,试写出满足条件的所有分派方案;
(3)农机租赁公司拟出一个分派方案,使该公司50台收割机每天获得租金最高,并说明理由.
13.设a=${∫}_{0}^{π}$$\sqrt{2}$cos(x-$\frac{π}{4}$)dx,则二项式(a$\sqrt{x}$-$\frac{1}{\sqrt{x}}$)4中展开式中含x项的系数是( )
| A. | -32 | B. | 32 | C. | -8 | D. | 8 |
6.设i为虚数单位,已知${z_1}=\frac{1-i}{1+i},{z_2}=-\frac{1}{2}+\frac{{\sqrt{3}}}{2}i$,则|z1|,|z2|的大小关系是( )
| A. | |z1|<|z2| | B. | |z1|=|z2| | C. | |z1|>|z2| | D. | 无法比较 |
