题目内容
已知过抛物线y2=2px(p>0)的焦点,斜率为2的直线交抛物线于A(x1,y1),B(x2,y2)(x1<x2)两点,且|AB|=9.
(1)求该抛物线的方程;
(2)O为坐标原点,C为抛物线上一点,若 =
= +λ
+λ ,求λ的值.
,求λ的值.
解析:(1)直线AB的方程是y=2 ,与y2=2px联立,从而有4x2-5px+p2=0,
,与y2=2px联立,从而有4x2-5px+p2=0,
所以x1+x2= .
.
由抛物线定义得|AB|=x1+x2+p=9,
所以p=4,从而抛物线方程是y2=8x.
(2)由p=4,4x2-5px+p2=0可简化为x2-5x+4=0,
从而x1=1,x2=4,y1=-2,y2=4,
从而A(1,-2),B(4,4).
 设
设 =(x3,y3)
=(x3,y3)
=(1,-2)+λ(4,4)
=(4λ+1,4λ-2),
又y =8x3,即[2(2λ-1)] 2=8(4λ+1),
=8x3,即[2(2λ-1)] 2=8(4λ+1),
即(2λ-1)2=4λ+1,
解得λ=0或λ=2.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
 的最大值是( ).
的最大值是( ). C.19 D.16
C.19 D.16 中,
中,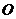 是坐标原点,两定点
是坐标原点,两定点 满足
满足 ,则点集
,则点集 所表示的区域的面积为( ).
所表示的区域的面积为( ). B.
B. C.
C. D.
D.
 的是 ( )
的是 ( ) B.
B. ,
,
 D.
D.
 1相切,则圆C的方程是______
1相切,则圆C的方程是______ 与直线
与直线 有两个不同的交点,则实数
有两个不同的交点,则实数 的取值范围是( )
的取值范围是( ) B.
B. C.
C. D.
D.
 与其关于点
与其关于点 对称的抛物线有两个不同的交点,若过这两个交点的直线的倾斜角为
对称的抛物线有两个不同的交点,若过这两个交点的直线的倾斜角为 ,则实数
,则实数 的值为______________.
的值为______________.