题目内容
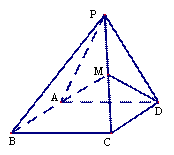
如图,四棱锥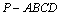 ,侧面
,侧面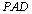 是边长为
是边长为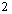 的正三角形,且与底面垂直,底面
的正三角形,且与底面垂直,底面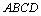 是
是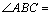
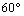 的菱形,
的菱形,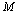 为棱
为棱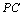 上的动点,且
上的动点,且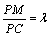 (
(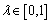 )。
)。
(Ⅰ) 求证: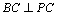 ;
;
(Ⅱ) 试确定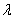 的值,使得二面角
的值,使得二面角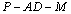 的平面角余弦值为
的平面角余弦值为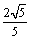 。
。
 |
解: (Ⅰ)取 中点
中点 ,连结
,连结 ,依题意可知△
,依题意可知△ ,△
,△ 均为正三角形,
均为正三角形,
 所以
所以 ,
, ,又
,又 ,
, ,
, 平面
平面 ,
,
所以 平面
平面 ,又
,又 平面
平面 ,所以
,所以 ,
,
因为 ,所以
,所以 。…………5分
。…………5分
(Ⅱ)由(Ⅰ)可知 ,又平面
,又平面 平面
平面 ,
,
平面 平面
平面
 ,
,
 平面
平面 ,所以
,所以 平面
平面 .…………6分
.…………6分
以 为原点,建立空间直角坐标系
为原点,建立空间直角坐标系 如图所示, …………7分
如图所示, …………7分
则 ,
, ,
, ,
, ,
,

由 可得点
可得点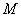 的坐标为
的坐标为 ,
,
所以 ,
, ,
,
设平面 的法向量为
的法向量为 ,则
,则 ,即
,即
解得 ,令
,令 ,得
,得 ,…………8分
,…………8分
显然平面 的一个法向量为
的一个法向量为 ,…………9分
,…………9分
依题意 ,………… 10分
,………… 10分
解得 或
或 (舍去), ………… 11分
(舍去), ………… 11分
所以,当 时,二面角
时,二面角 的余弦值为
的余弦值为 .………… 12分
.………… 12分

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
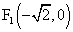 ,
,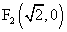 ,且
,且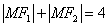
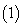 求动点M轨迹
求动点M轨迹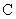 的方程;
的方程;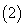 设
设 为坐标原点,若点
为坐标原点,若点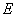 在轨迹
在轨迹 在直线
在直线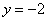 上,且
上,且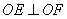 ,试判断直线
,试判断直线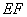 与圆
与圆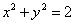 的位置关系,并说明理由.
的位置关系,并说明理由.
 构成平面区域
构成平面区域 (其中
(其中 ,
, 是变量)。若目标函数
是变量)。若目标函数 的最小值为-6,则实数
的最小值为-6,则实数 的值为( )
的值为( ) B.6 C.3 D.
B.6 C.3 D.
 是图中边长为4的正方形区域,
是图中边长为4的正方形区域, 是
是 图象下方的点构成的区域.在
图象下方的点构成的区域.在
 的解集为
的解集为

 的渐近线与圆C: (x-
的渐近线与圆C: (x- )2+y2=1相切,则双曲线的离心率是 ( )
)2+y2=1相切,则双曲线的离心率是 ( ) D.
D. 在(
在( ,
, )上既是奇函数又是增函数,则函数
)上既是奇函数又是增函数,则函数 的图象是 ( )
的图象是 ( )
 上的可导函数
上的可导函数 的导函数
的导函数 的图象如左所示,则
的图象如左所示,则