题目内容
 如图,已知|
如图,已知|| OA |
| OB |
| 3 |
| OA |
| OB |
| 5π |
| 6 |
 |
| AB |
| OA |
| OC |
考点:平面向量数量积的运算
专题:平面向量及应用
分析:建立直角坐标系,写出A(1,0),B(-
,
),C(0,0),求出圆的方程为:x2+y2+Dx+Ey+F=0则
•
=x,即圆上的点的横坐标.
| 3 |
| 2 |
| ||
| 2 |
| OA |
| OC |
解答:
 解:建立直角坐标系,则A(1,0),B(-
解:建立直角坐标系,则A(1,0),B(-
,
),C(0,0),
设C(x,y),圆的方程为:x2+y2+Dx+Ey+F=0,
将A(1,0),B(-
,
),C(x,y)代入圆的方程,解得
D=-1,E=-3
,F=0;
∴x2+y2-x+-3
y+=0,
表示圆心为(
,
),半径为
,
•
=x,
∴x的最大值为
+
,
故答案为:
+
.
 解:建立直角坐标系,则A(1,0),B(-
解:建立直角坐标系,则A(1,0),B(-| 3 |
| 2 |
| ||
| 2 |
设C(x,y),圆的方程为:x2+y2+Dx+Ey+F=0,
将A(1,0),B(-
| 3 |
| 2 |
| ||
| 2 |
D=-1,E=-3
| 3 |
∴x2+y2-x+-3
| 3 |
表示圆心为(
| 1 |
| 2 |
3
| ||
| 2 |
| 7 |
| OA |
| OC |
∴x的最大值为
| 1 |
| 2 |
| 7 |
故答案为:
| 1 |
| 2 |
| 7 |
点评:本题考查圆的方程及向量的数量积,考查利用代数解决几何问题的方法,属于基础题.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
执行如图程序框图,如果输入的依次为3,5,3,5,5,4,4,3,4,4,则输出的s为( )

A、
| ||||
| B、4 | ||||
C、
| ||||
D、
|
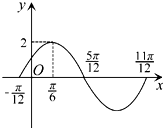 函数y=2sin(ωx+φ)(ω>0,|φ|<
函数y=2sin(ωx+φ)(ω>0,|φ|<
 一个三棱锥的三视图如图所示,其正视图、左视图、俯视图的面积分别是1,2,4,则这个三棱锥的表面积为
一个三棱锥的三视图如图所示,其正视图、左视图、俯视图的面积分别是1,2,4,则这个三棱锥的表面积为