题目内容
9.在复平面内,复数$\frac{2}{1+i}$(i为虚数单位)对应的点与原点的距离是$\sqrt{2}$.分析 利用复数代数形式乘除运算化简求得复数$\frac{2}{1+i}$对应的点的坐标,再由两点间的距离公式求解.
解答 解:∵$\frac{2}{1+i}$=$\frac{2(1-i)}{(1+i)(1-i)}=1-i$,
∴复数$\frac{2}{1+i}$对应的点的坐标为(1,-1),与原点的距离是$\sqrt{{1}^{2}+(-1)^{2}}=\sqrt{2}$.
故答案为:$\sqrt{2}$.
点评 本题考查复数代数形式的乘除运算,考查了复数的代数表示法及其几何意义,是基础题.

练习册系列答案
相关题目
20.某市拟招商引资兴建一化工园区,新闻媒体对此进行了问卷调查,在所有参与调查的市民中,持“支持”、“保留”和“不支持”态度的人数如表所示:
(Ⅰ)在所有参与调查的人中,用分层抽样的方法抽取部分市民做进一步调研(不同态度的群体中亦按年龄分层抽样),已知从“保留”态度的人中抽取了19人,则在“支持”态度的群体中,年龄在30岁以上的人有多少人被抽取;
(Ⅱ)在持“不支持”态度的人中,用分层抽样的方法抽取6人做进一步的调研,将此6人看作一个总体,在这6人中任意选取2人,求至少有1人在30岁以上的概率.
| 支持 | 保留 | 不支持 | |
| 30岁以下 | 900 | 120 | 280 |
| 30岁以上(含30岁) | 300 | 260 | 140 |
(Ⅱ)在持“不支持”态度的人中,用分层抽样的方法抽取6人做进一步的调研,将此6人看作一个总体,在这6人中任意选取2人,求至少有1人在30岁以上的概率.
17.已知数列{an}的前n项和为Sn,且Sn=2an-1,则$\frac{S_6}{a_6}$=( )
| A. | $\frac{63}{32}$ | B. | $\frac{31}{16}$ | C. | $\frac{123}{64}$ | D. | $\frac{127}{128}$ |
4.从长方体一个顶点出发的三条棱长分别为2、3、4,则其对角线的长为( )
| A. | 3 | B. | 5 | C. | $\sqrt{26}$ | D. | $\sqrt{29}$ |
18.计算log232•log327=(( )
| A. | 12 | B. | 10 | C. | 15 | D. | 18 |
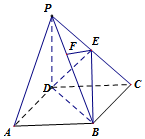 在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,点E是PC的中点,作EF⊥PB交PB于点F.
在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,点E是PC的中点,作EF⊥PB交PB于点F.