题目内容
6.函数$f(x)=sin2x+\sqrt{3}cos2x$在区间[0,π]上的零点之和是( )| A. | $\frac{2π}{3}$ | B. | $\frac{7π}{12}$ | C. | $\frac{7π}{6}$ | D. | $\frac{4π}{3}$ |
分析 由f(x)=0结合正切函数的性质求出函数的零点即可得到结论.
解答 解:由$f(x)=sin2x+\sqrt{3}cos2x$=0得sin2x=-$\sqrt{3}$cos2x,
即tan2x=-$\sqrt{3}$,
即2x=kπ-$\frac{π}{3}$,
即x=$\frac{kπ}{2}$-$\frac{π}{6}$,
∵0≤x≤π,
∴当k=1时,x=$\frac{π}{3}$,
当k=2时,x=$\frac{5π}{6}$,
则函数f(x)的零点之和为$\frac{π}{3}$+$\frac{5π}{6}$=$\frac{7π}{6}$,
故选:C
点评 本题主要考查函数零点的求解和应用,根据正切函数的性质求出x的值是解决本题的关键.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
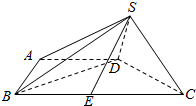 如图,四棱锥S-ABCD中,BC∥AD,BC=2AB=2AD=2,SD=$\frac{1}{2}$,BD⊥SD,∠ABC=60°,E为BC的中点.
如图,四棱锥S-ABCD中,BC∥AD,BC=2AB=2AD=2,SD=$\frac{1}{2}$,BD⊥SD,∠ABC=60°,E为BC的中点.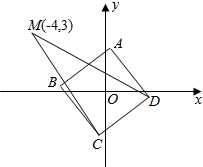 如图所示,ABCD是以原点O为中心、边长为2的正方形,M点坐标为(-4,3),当正方形在满足上述条件下转动时,$\overrightarrow{MC}•\overrightarrow{MD}$的取值范围是[15,35].
如图所示,ABCD是以原点O为中心、边长为2的正方形,M点坐标为(-4,3),当正方形在满足上述条件下转动时,$\overrightarrow{MC}•\overrightarrow{MD}$的取值范围是[15,35].