题目内容
(I)求值:
-20130;
(Ⅱ)设函数f(x)是定义在R上的偶函数,且f(x)=f(x-2),当x∈[0,1]时,f(x)=x+1,求f(
)的值.
log23+log2
| ||
log29-log2
|
(Ⅱ)设函数f(x)是定义在R上的偶函数,且f(x)=f(x-2),当x∈[0,1]时,f(x)=x+1,求f(
| 3 |
| 2 |
考点:函数的周期性,对数的运算性质
专题:计算题
分析:(I)利用对数的运算性质,分别计算即可,结合a0=1,即可得到答案;
(Ⅱ)根据题意,可以确定函数的周期性,利用函数的周期性和奇偶性,将f(
)转化为f(
)求解即可.
(Ⅱ)根据题意,可以确定函数的周期性,利用函数的周期性和奇偶性,将f(
| 3 |
| 2 |
| 1 |
| 2 |
解答:
解:(I)
-20130
=
-1
=
-1
=1-1
=0;
(Ⅱ)∵f(x)=f(x-2),
∴f(x+2)=f(x),
故函数f(x)是周期函数,且周期为2,
又∵函数f(x)为偶函数,且当x∈[0,1]时,f(x)=x+1,
∴f(
)=f(
-2)=f(-
)=f(
)=
+1=
.
故f(
)=
.
log23+log2
| ||
log29-log2
|
=
log2(3×
| ||||
log2
|
=
log23
| ||
log23
|
=1-1
=0;
(Ⅱ)∵f(x)=f(x-2),
∴f(x+2)=f(x),
故函数f(x)是周期函数,且周期为2,
又∵函数f(x)为偶函数,且当x∈[0,1]时,f(x)=x+1,
∴f(
| 3 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
故f(
| 3 |
| 2 |
| 3 |
| 2 |
点评:本题考查了对数的运算性质,考查了函数的求值以及函数性质的应用.解题时要注意非零实数的零次幂等于1,考查了函数的周期性和奇偶性的综合应用,要熟练掌握函数的性质的综合应用.属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
甲、乙两人同时从图书馆走向教室,甲一半路程步行,一半路程跑步;乙一半时间步行,一半时间跑步,若两人步行、跑步的速度一样,则先到教室的是( )
| A、甲 | B、乙 |
| C、甲、乙同时到达 | D、无法确定 |
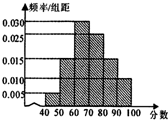 某校从高一年级学生中随机抽取部分学生,将他们的模块测试成绩分为6组:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]加以统计,得到如图所示的频率分布直方图,已知高一年级共有学生600名,据此估计,该模块测试成绩不少于60分的学生人数为
某校从高一年级学生中随机抽取部分学生,将他们的模块测试成绩分为6组:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]加以统计,得到如图所示的频率分布直方图,已知高一年级共有学生600名,据此估计,该模块测试成绩不少于60分的学生人数为