题目内容
已知函数f(x)=log2x-x+1,数列{an}满足a1=2,
=2(n∈N*).
(1)求数列{an}的通项公式an;
(2)设bn=f(an)求数列{bn}的前n项和Sn.
| an+1 |
| an |
(1)求数列{an}的通项公式an;
(2)设bn=f(an)求数列{bn}的前n项和Sn.
考点:数列的求和
专题:等差数列与等比数列
分析:(1)首先根据递推关系式,求出数列为等比数列,进一步求出通项公式.
(2)利用(1)的结论,再根据已知条件,利用分类法求数列的和.
(2)利用(1)的结论,再根据已知条件,利用分类法求数列的和.
解答:
解:(1)∵
=2,
∴{an}是公比为2首项为2的等比数列,
∴an=2×2n-1=2n(n=1),此式也满足)
∴an═2n
(2)由(1)知
f(an)=log22n-2n+1=(n+1)-2n,
∴f(a1)+f(a2)+…+f(an)=[2+3+…+(n+1)]-(2+22+…2n)
=
-2n+1+2.
| an+1 |
| an |
∴{an}是公比为2首项为2的等比数列,
∴an=2×2n-1=2n(n=1),此式也满足)
∴an═2n
(2)由(1)知
f(an)=log22n-2n+1=(n+1)-2n,
∴f(a1)+f(a2)+…+f(an)=[2+3+…+(n+1)]-(2+22+…2n)
=
| n(n+3) |
| 2 |
点评:本题考查的知识要点:等比数列的通项公式,利用分类的方法求数列的和.属于基础题型.

练习册系列答案
相关题目
设M(x,y)是区域
内的动点,且不等式x+2y≤14恒成立,则实数a的取值范围是( )
|
| A、[8,10] |
| B、[8,9] |
| C、[6,9] |
| D、[6,10] |
若点P(m,n)Q(n-1,m+1)关于直线l对称,则l的方程是( )
| A、x-y+1=0 |
| B、x-y=0 |
| C、x+y+1=0 |
| D、x+y=0 |
函数f(x)=sin(-2x)的一个单调增区间是( )
A、[-
| ||||
B、[-
| ||||
C、[-
| ||||
D、[-
|
将函数y=sin(x-
)上各点的纵坐标不变,横坐标伸长位为原来的2倍,然后将图象沿x轴向左平移π个单位,与所得新图象对应的解析式为( )
| π |
| 3 |
A、y=sin(2x+
| ||||
B、y=sin(2x+
| ||||
C、y=sin(
| ||||
D、y=sin(
|
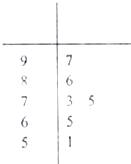 某校高一级数学必修一模块考试的成绩分为四个等级,85分-100分为A等,70分-84分为B等,55分-69分为C等,54分以下为D等.右边的茎叶图(十位为茎,个位为叶)记录了某班某小组6名学生的数学必修一模块考试成绩.
某校高一级数学必修一模块考试的成绩分为四个等级,85分-100分为A等,70分-84分为B等,55分-69分为C等,54分以下为D等.右边的茎叶图(十位为茎,个位为叶)记录了某班某小组6名学生的数学必修一模块考试成绩.