题目内容
函数y=sin(x+
)+cos(x+
)的最大值为 .
| π |
| 6 |
| π |
| 3 |
考点:两角和与差的正弦函数,三角函数的最值
专题:三角函数的求值
分析:利用两角和公式对函数解析式分解整理,利用余弦函数的性质求得函数的最大值.
解答:
解:y=sin(x+
)+cos(x+
)=
sinx+
cosx+
cosx-
sinx=cosx,
∵cosx≤1,
∴函数y的最大值为1.
故答案为:1
| π |
| 6 |
| π |
| 3 |
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
∵cosx≤1,
∴函数y的最大值为1.
故答案为:1
点评:本题主要考查了两角和公式的化简和求值.属基础题.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
已知一组数据:1,2,1,3,3.这组数据的方差是( )
| A、4 | ||||
| B、5 | ||||
| C、0.8 | ||||
D、
|
已知a<b<0,则下列不等式一定成立的是( )
A、
| ||||
| B、|a|>-b | ||||
C、
| ||||
D、
|
某校打算从高一年级800名学生中抽取80名学生进行问卷调查,如果采用系统抽样的方法,则抽样的分段间隔应为( )
| A、20 | B、10 | C、8 | D、5 |
已知{an},{bn}都是等比数列,它们的前n项和分别为Sn,Tn,且
=
对n∈N*恒成立,则
=( )
| Sn |
| Tn |
| 3n+1 |
| 4 |
| an+1 |
| bn+1 |
| A、3n | ||
| B、4n | ||
| C、3n或4n | ||
D、(
|
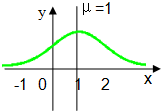 在对我市高中学生某项身体素质的测试中,测试结果ξ服从正态分布N(1,σ2)(σ>0)(如图),若ξ在(0,2)内取值的概率为0.8,则ξ在(0,1)内取值的概率为
在对我市高中学生某项身体素质的测试中,测试结果ξ服从正态分布N(1,σ2)(σ>0)(如图),若ξ在(0,2)内取值的概率为0.8,则ξ在(0,1)内取值的概率为