题目内容
9.已知函数f(x)=|kx-2|+|kx-k|,g(x)=x+3.(1)当k=1时,求不等式f(x)≥g(x)的解集;
(2)若对任意的x∈R,f(x)≥4都成立,求实数k的取值范围.
分析 (1)把要解的不等式等价转化为与之等价的三个不等式组,求出每个不等式组的解集,再取并集,即得所求.
(2)由题意|x-$\frac{2}{k}$|+|x-1|≥$\frac{4}{|k|}$ 恒成立,再利用绝对值不等式可得|1-$\frac{2}{k}$|≥$\frac{4}{|k|}$,故|k-2|≥4,由此求得k的范围.
解答 解:(1)∵函数f(x)=|kx-2|+|kx-k|,g(x)=x+3.
当k=1时,不等式f(x)≥g(x),即|x-2|+|x-1|≥x+3,
即$\left\{\begin{array}{l}{x<1}\\{2-x+1-x≥x+3}\end{array}\right.$ ①,或$\left\{\begin{array}{l}{1≤x≤2}\\{2-x+x-1≥x+3}\end{array}\right.$②,或 $\left\{\begin{array}{l}{x>2}\\{x-2+x-1≥x+3}\end{array}\right.$③.
解①求得 x≤0,解②求得x无解,解③求得x>2,
综上可得,原不等式的解集为{x|x≤0或x>2}.
(2)若对任意的x∈R,f(x)≥4都成立,即|kx-2|+|kx-k|≥4 恒成立,∵k≠0,
即|x-$\frac{2}{k}$|+|x-1|≥$\frac{4}{|k|}$ 恒成立,
故h(x)=|x-$\frac{2}{k}$|+|x-1|的最小值大于或等于$\frac{4}{|k|}$.
∵h(x)=|x-$\frac{2}{k}$|+|x-1|≥|(x-$\frac{2}{k}$)-(x-1)|=|1-$\frac{2}{k}$|,∴|1-$\frac{2}{k}$|≥$\frac{4}{|k|}$,|k-2|≥4,
即k-2≥4,或k-2≤-4,∴k≥6 或k≤-2,
故实数k的取值范围为{x|k≥6 或k≤-2}.
点评 本题主要考查绝对值不等式的解法,函数的恒成立问题,绝对值三角不等式的应用,体现了转化、分类讨论的数学思想,属于中档题.

| A. | (3,4) | B. | (-3,2) | C. | (-1,0) | D. | (5,-6) |
| A. | 23 | B. | 95 | C. | 135 | D. | 138 |
| A. | (-$\frac{1}{2}$)2015 | B. | ($\frac{1}{2}$)2015 | C. | ($\frac{1}{2}$)2014 | D. | (-$\frac{1}{2}$)2014 |
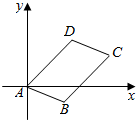 如图,已知平行四边形ABCD的三个顶点的坐标分别为A(0,0),B(2,-1),C(4,2).
如图,已知平行四边形ABCD的三个顶点的坐标分别为A(0,0),B(2,-1),C(4,2).