题目内容
5. 如图,两同心圆(圆心在原点)分别与OA、OB交于A、B两点,其中A($\sqrt{2}$,1),|OB|=$\sqrt{6}$,阴影部分为两同心圆构成的扇环,已知扇环的面积为$\frac{3π}{4}$.
如图,两同心圆(圆心在原点)分别与OA、OB交于A、B两点,其中A($\sqrt{2}$,1),|OB|=$\sqrt{6}$,阴影部分为两同心圆构成的扇环,已知扇环的面积为$\frac{3π}{4}$.(1)设角θ的始边为x轴的正半轴,终边为OA,求$\frac{tan(π-θ)cos(θ+\frac{3π}{2})}{sin(2θ-π)}$的值;
(2)求点B的坐标.
分析 (1)根据A点坐标求出θ的三角函数,利用诱导公式化简;
(2)根据扇环面积求出圆心角,得出∠xOB对应的角,利用三角函数求出B的坐标.
解答 解:(1)∵tanθ=$\frac{1}{\sqrt{2}}=\frac{\sqrt{2}}{2}$,∴sinθ=$\frac{\sqrt{3}}{3}$,cos$θ=\frac{\sqrt{6}}{3}$.
∴$\frac{tan(π-θ)cos(θ+\frac{3π}{2})}{sin(2θ-π)}$=$\frac{-tanθsinθ}{-sin2θ}=\frac{tanθ}{2cosθ}$=$\frac{\sqrt{3}}{4}$.
(2)|OA|=$\sqrt{2+1}=\sqrt{3}$,设∠AOB=α,
则$\frac{1}{2}$α(|OB|2-|OA|2)=$\frac{3π}{4}$.
解得α=$\frac{π}{2}$.
∴$\sqrt{6}$cos($θ+\frac{π}{2}$)=-$\sqrt{6}$sinθ=-$\sqrt{2}$,$\sqrt{6}$sin($θ+\frac{π}{2}$)=$\sqrt{6}$cosθ=2.
∴B点坐标为B(-$\sqrt{2}$,2).
点评 本题考查了三角函数的计算,化简求值,属于基础题.

练习册系列答案
相关题目
17.空间9个点分布异面直线L1、L2上,L1上有4个点,L2上有5个点,则由它们可确定异面直线的对数为( )
| A. | 121对 | B. | 108对 | C. | 21对 | D. | 60对 |
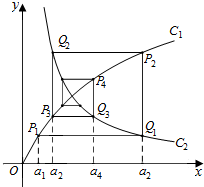 如图,已知曲线C1:y=$\frac{2x}{x+1}$(x>0)及曲线C2:y=$\frac{1}{3x}$(x>0),C1上的点P1的横坐标为a1(0<a1<$\frac{1}{2}$).从C1上的点Pn(n∈N+)作直线平行于x轴,交曲线C2于点Qn,再从点Qn作直线平行于y轴,交曲线C1于点Pn+1.点Pn(n=1,2,3,…)的横坐标构成数列{an}
如图,已知曲线C1:y=$\frac{2x}{x+1}$(x>0)及曲线C2:y=$\frac{1}{3x}$(x>0),C1上的点P1的横坐标为a1(0<a1<$\frac{1}{2}$).从C1上的点Pn(n∈N+)作直线平行于x轴,交曲线C2于点Qn,再从点Qn作直线平行于y轴,交曲线C1于点Pn+1.点Pn(n=1,2,3,…)的横坐标构成数列{an}