题目内容
14.设抛物线y2=4mx(m>0)的准线与x轴交于F1,焦点为F2;以F1、F2为焦点,离心率e=$\frac{1}{2}$的椭圆与抛物线的一个交点为$E(\frac{2}{3},\frac{{2\sqrt{6}}}{3})$;自F1引直线交抛物线于P、Q两个不同的点,点P关于x轴的对称点记为M,设$\overrightarrow{{F_1}P}=λ\overrightarrow{{F_1}Q}$.(Ⅰ)求抛物线的方程和椭圆的方程;
(Ⅱ)求证:$\overrightarrow{{F_2}M}=-λ\overrightarrow{{F_2}Q}$.
分析 (Ⅰ)设椭圆的方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),运用离心率公式和点满足椭圆方程,解方程可得a,b,进而得到椭圆的方程;再由焦点坐标可得m=1,进而得到抛物线的方程;
(Ⅱ)记P(x1,y1)、Q(x2,y2)、M(x1,-y1),由向量共线的坐标表示,结合分析法和联立直线方程和抛物线的方程,运用韦达定理即可得证.
解答 解:(Ⅰ)设椭圆的方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),
由E在椭圆上,得$\frac{4}{{9{a^2}}}+\frac{24}{{9{b^2}}}=1$①,
e=$\frac{c}{a}$=$\frac{\sqrt{{a}^{2}-{b}^{2}}}{a}$=$\frac{1}{2}$ ②
由①、②解得a2=4,b2=3,
椭圆的方程为$\frac{x^2}{4}+\frac{y^2}{3}=1$;
可得焦点为F1(-1,0),F2(1,0),
可得抛物线y2=4mx(m>0)的准线为x=-m,
即有m=1,易得抛物线的方程是:y2=4x;
(Ⅱ)证明:记P(x1,y1)、Q(x2,y2)、M(x1,-y1),
由$\overrightarrow{{F_1}P}=λ\overrightarrow{{F_1}Q}$得x1+1=λ(x2+1),
于是有λ=$\frac{{x}_{1}+1}{{x}_{2}+1}$,①
欲证:$\overrightarrow{{F_2}M}=-λ\overrightarrow{{F_2}Q}$,只需证:$λ=\frac{{{x_1}-1}}{{1-{x_2}}}$,②
由①②知:只需证明:$\frac{{{x_1}-1}}{{1-{x_2}}}$=$\frac{{{x_1}+1}}{{{x_2}+1}}$,
化简为:x1x2=1,
设直线PQ的方程为y=k(x+1),
与抛物线的方程联立,得:k2x2+(2k2-4)x+k2=0,
根据韦达定理:x1+x2=$\frac{{2{k^2}-4}}{k^2}$,x1x2=1,
根据以上步骤可知:$\overrightarrow{{F_2}M}=-λ\overrightarrow{{F_2}Q}$成立.
点评 本题考查椭圆和抛物线的方程的求法,注意运用离心率公式和点满足椭圆方程,以及抛物线的性质,考查向量共线的证明,注意运用分析法和联立方程,结合韦达定理,属于中档题.

 名校通行证有效作业系列答案
名校通行证有效作业系列答案
| A. | 22+$\frac{2}{3}$π | B. | 22+$\frac{5}{3}$π | C. | 22+$\frac{8}{3}$π | D. | 22-π |
| A. | (-∞,-$\sqrt{6}$)∪($\sqrt{6}$,+∞) | B. | ($\sqrt{6}$,$\frac{5}{2}$) | C. | (2,4) | D. | ($\sqrt{6}$,$\frac{11}{4}$] |
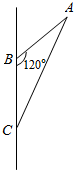 如图所示,在△ABC中,AB=2,BC=2,∠ABC=120°,若将△ABC绕BC旋转一周,求所形成的旋转体的表面积和体积.
如图所示,在△ABC中,AB=2,BC=2,∠ABC=120°,若将△ABC绕BC旋转一周,求所形成的旋转体的表面积和体积.