题目内容
5．已知关于x的不等式|x-2|≤a（a＞0）恰有5个整数解，则实数a的取值范围是[2，3）．分析 根据不等式求出不等式的范围，结合绝对值的几何意义进行求解即可．
解答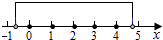 
解：∵|x-2|≤a，
∴-a≤x-2≤a，
即2-a≤x≤2+a，
若不等式|x-2|≤a（a＞0）恰有5个整数解，
则这5个整数解为0，1，2，3，4，
则满足$\left\{\begin{array}{l}{-1＜2-a≤0}\\{4≤2+a＜5}\end{array}\right.$，
即$\left\{\begin{array}{l}{2≤a＜3}\\{2≤a＜3}\end{array}\right.$，
解得2≤a＜3，
故答案为：[2，3）
点评 本题主要考查不等式解的应用，利用绝对值的几何意义建立不等式关系是解决本题的关键．
练习册系列答案
相关题目
15．过点P（2，3）并且在两坐标轴上截距相等的直线方程为（ ）
| A． | 2x-3y=0 | B． | 3x-2y=0或x+y-5=0 | ||
| C． | x+y-5=0 | D． | 2x-3y=0或x+y-5=0 |
10．已知命题P的逆命题是“若a、b都不是偶数，则ab不是偶数”，则命题P的逆否命题是（ ）
| A． | 若a、b都是偶数，则ab是偶数 | |
| B． | 若ab是偶数，则a、b都是偶数 | |
| C． | 若a、b至少有一个是偶数，则ab是偶数 | |
| D． | 若ab是偶数，则a、b至少有一个是偶数 |