题目内容
已知圆M:x2+y2-4x-8y+m=0与x轴相切.
(1)求m的值;
(2)求圆M在y轴上截得的弦长.
(1)求m的值;
(2)求圆M在y轴上截得的弦长.
考点:直线与圆的位置关系
专题:直线与圆
分析:(1)求出圆的圆心坐标,利用圆M:x2+y2-4x-8y+m=0与x轴相切,即可求m的值;
(2)利用x=0,求圆M在y轴的交点纵坐标,即可求解圆M在y轴上截得的弦长.
(2)利用x=0,求圆M在y轴的交点纵坐标,即可求解圆M在y轴上截得的弦长.
解答:
解:(1)圆M:x2+y2-4x-8y+m=0化为圆M:(x-2)2+(y-4)2=20-m,
圆的圆心坐标(2,4),半径为
,
∵圆M:x2+y2-4x-8y+m=0与x轴相切,
∴
=4,解得m=4.
(2)圆M:x2+y2-4x-8y+4=0,
当x=0时,可得y2-8y+4=0,解得y1=4+2
或y2=4-2
.
圆M在y轴上截得的弦长:y1-y2=4+2
-4+2
=4
.
圆的圆心坐标(2,4),半径为
| 20-m |
∵圆M:x2+y2-4x-8y+m=0与x轴相切,
∴
| 20-m |
(2)圆M:x2+y2-4x-8y+4=0,
当x=0时,可得y2-8y+4=0,解得y1=4+2
| 3 |
| 3 |
圆M在y轴上截得的弦长:y1-y2=4+2
| 3 |
| 3 |
| 3 |
点评:本题考查直线与圆的位置关系,切线方程的应用,考查计算能力.

练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目
过点(3,1)作圆(x+1)2+y2=1的两条切线,切点分别为A,B,则直线AB的方程为( )
A、2x+y-
| ||
B、2x-y-
| ||
C、4x-y-
| ||
D、4x+y-
|
已知函数y=f(x)的图象与函数y=ax(a>0且a≠1)的图象关于直线y=x对称,记g(x)=f(x)[f(x)+2f(2)-1],若y=g(x)在区间[
,2]上是增函数,则实数a的取值范围是( )
| 1 |
| 2 |
| A、[2,+∞) | ||
| B、(0,1)∪(1,2) | ||
C、[
| ||
D、(0,
|
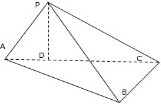 如图,在三棱锥P-ABC中,PD⊥面ABC于点D,且点D在AC上,PA=PB=PC=3,设AB=BC=
如图,在三棱锥P-ABC中,PD⊥面ABC于点D,且点D在AC上,PA=PB=PC=3,设AB=BC=