题目内容
选修4—5:不等式选讲
设不等式 的解集为
的解集为 , 且
, 且 .
.
(Ⅰ) 试比较 与
与 的大小;
的大小;
(Ⅱ) 设 表示数集
表示数集 中的最大数, 且
中的最大数, 且 , 求
, 求 的范围.
的范围.
(Ⅰ) ;(Ⅱ)
;(Ⅱ) .
.
【解析】
试题分析:(Ⅰ)首先解绝对值的不等式求得集合 ,进而确定
,进而确定 的范围,再利用作差法(与零比较),得到
的范围,再利用作差法(与零比较),得到 与
与 两个数的大小;(Ⅱ)
两个数的大小;(Ⅱ) 表示三个数中最大的数,所以
表示三个数中最大的数,所以 比三个数都大或等,即
比三个数都大或等,即 ,三式相乘,利用基本不等式进一步得到
,三式相乘,利用基本不等式进一步得到 (当且仅当“
(当且仅当“ ”时取等号),得到
”时取等号),得到 的取值范围.
的取值范围.
试题解析:(Ⅰ) ,
,


 4分
4分
(Ⅱ) ,
,
 10分
10分
考点:1.含绝对值的不等式;2.基本不等式.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案
相关题目
 本不同的数学书和
本不同的数学书和 本语文书在书架上随机排成一行,则
本语文书在书架上随机排成一行,则 本数学书相邻的概率为
本数学书相邻的概率为  满足
满足 ,且当
,且当 时,
时, ,则
,则 与
与 的图象的交点个数为( )
的图象的交点个数为( ) (B)
(B) (C)
(C) (D)
(D) 
 和曲线
和曲线 围成的图形的面积是________.
围成的图形的面积是________. ,若X在(0,8)内取值的概率为0.6,则X在(0,4)内取值的概率为
,若X在(0,8)内取值的概率为0.6,则X在(0,4)内取值的概率为 中,
中, ,
,  ,平面
,平面 平面
平面 ,
, 与
与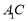 相交于点
相交于点 .
.
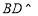 平面
平面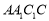 ;
;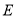 是直线
是直线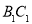 上一点,且
上一点,且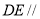 平面
平面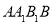 ,求平面
,求平面 与平面
与平面 夹角的余弦值.
夹角的余弦值.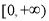 上的函数
上的函数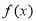 满足
满足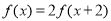 ,当
,当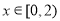 时,
时,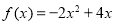 .
.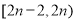 上的最大值为
上的最大值为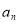 (
(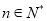 ),且
),且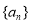 的前
的前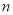 项和为
项和为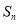 ,则
,则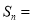 ( )
( )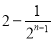 B.
B.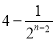 C.
C.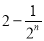 D.
D.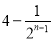
 ,acosA=bcosB.
,acosA=bcosB.

 为第三项,3为第六项的等比数列的公比,则
为第三项,3为第六项的等比数列的公比,则 ________.
________.