题目内容
20.已知函数f(x)=x3+ax2-x+c(x∈R),下列结论错误的是( )| A. | 函数f(x)一定存在极大值和极小值 | |
| B. | 若函数f(x)在(-∞,x1),(x2,+∞)上是增函数,则x2-x1≥$\frac{2\sqrt{3}}{3}$ | |
| C. | 函数f(x)的图象是中心对称图形 | |
| D. | 函数f(x)的图象在点(x0,f(x0))(x0∈R)处的切线与f(x)的图象必有两个不同的公共点 |
分析 先求出函数的导数,找到单调区间,列出表格,逐一排除,得出答案.
解答 解:∵f′(x)=3x2+2ax-1.
∴△=4a2+12>0,
∴f′(x)=0有两解,不妨设为x1<x2,列表如下
| x | (-∞,x1) | x1 | (x1,x2) | x2 | (x2,+∞) |
| f'(x) | + | 0 | - | 0 | + |
| f(x) | 单调递增 | 极大值 | 单调递减 | 极小值 | 单调递增 |
①x=x1时,函数f(x)取到极大值,x=x2时,函数f(x)取到极小值,故选项A正确,
②函数f(x)在(-∞,x1),(x2,+∞)上是增函数,x2-x1=$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\frac{2\sqrt{{a}^{2}+3}}{3}$≥$\frac{2\sqrt{3}}{3}$,故选项B正确,
③∵f(-$\frac{2}{3}$a-x)+f(x)=$\frac{4{a}^{3}}{9}$+$\frac{2a}{3}$,f(-$\frac{a}{3}$)=$\frac{2{a}^{3}}{9}$+$\frac{a}{3}$,∴f(-$\frac{2}{3}$a-x)+f(x)=2f(-$\frac{a}{3}$),∴(-$\frac{a}{3}$,f(-$\frac{a}{3}$))为对称中心,故选项C正确,
选项A,B,C都正确,利用排除法,选项D错误,
即函数f(x)在点(x0,f(x0))处的切线与f(x)的图象可以有一个不同公共点.
故选:D.
点评 本题考察了函数的单调性,函数的最值问题,导数的应用,是一道综合题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.己知抛物线x2=2ay(a为常数)的准线经过点(1,-1),则抛物线的焦点坐标为( )
| A. | (-1,0) | B. | (1,0) | C. | (0,-1) | D. | (0,1) |
9.圆C:x2+y2=1,直线l:y=kx+2,直线l与圆C交与A,B,若|$\overrightarrow{OA}$$+\overrightarrow{OB}$|<|$\overrightarrow{OA}$$-\overrightarrow{OB}$|(其中O为坐标原点),则k的取值范围是( )
| A. | (0,$\sqrt{7}$) | B. | (-$\sqrt{7}$,$\sqrt{7}$) | C. | ($\sqrt{7}$,+∞) | D. | ($-∞,-\sqrt{7}$)$∪(\sqrt{7,}+∞)$ |
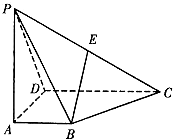 如图,四棱锥P-ABCD的底面ABCD为一直角梯形,其中BA⊥AD,CD⊥AD,CD=AD=2AB=2,PA⊥底面ABCD,E是PC的中点.
如图,四棱锥P-ABCD的底面ABCD为一直角梯形,其中BA⊥AD,CD⊥AD,CD=AD=2AB=2,PA⊥底面ABCD,E是PC的中点.