题目内容
5．{an}是等比数列，若a1=2，an=22n-1，求这个数列的前n项和Sn．分析 通过an=22n-1可知公比q=4，进而可知数列{an}是以2为首项、4为公比的等比数列，利用等比数列的求和公式计算即得结论．
解答 解：依题意，公比q=$\frac{{a}_{n+1}}{{a}_{n}}$=$\frac{{2}^{2（n+1）-1}}{{2}^{2n-1}}$=4，
则数列{an}是以2为首项、4为公比的等比数列，
于是Sn=$\frac{2（1-{4}^{n}）}{1-4}$=$\frac{{-2+2}^{2n+1}}{3}$．
点评 本题考查数列的求和，注意解题方法的积累，属于基础题．
练习册系列答案
优质课堂快乐成长系列答案
相关题目
15．若函数f（x）=ex-ax2有三个不同零点，则a的取值范围是（ ）
| A． | （$\frac{e^2}{4}$，+∞） | B． | （$\frac{{{e^{\;}}}}{2}$，+∞） | C． | （1，$\frac{e^2}{4}$） | D． | （1，$\frac{{{e^{\;}}}}{2}$） |
20．已知函数f（x）=x3+ax2-x+c（x∈R），下列结论错误的是（ ）
| A． | 函数f（x）一定存在极大值和极小值 | |
| B． | 若函数f（x）在（-∞，x1），（x2，+∞）上是增函数，则x2-x1≥$\frac{2\sqrt{3}}{3}$ | |
| C． | 函数f（x）的图象是中心对称图形 | |
| D． | 函数f（x）的图象在点（x0，f（x0））（x0∈R）处的切线与f（x）的图象必有两个不同的公共点 |
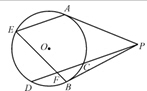过圆O外一点P向圆引两条切线PA、PB和割线PCD，从A点作弦AE平行于CD，连接BE交CD于F．