题目内容
17.比较${∫}_{0}^{3}$$\sqrt{5-\frac{5}{9}{x}^{2}}$dx与${∫}_{0}^{3}$$\sqrt{3-\frac{1}{3}{x}^{2}}$dx的大小.分析 由定积分的几何意义和椭圆的知识可得.
解答 解:由y=$\sqrt{5-\frac{5}{9}{x}^{2}}$平方整理可得$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{5}$=1,
∴${∫}_{0}^{3}$$\sqrt{5-\frac{5}{9}{x}^{2}}$dx表示椭圆$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{5}$=1的四分之一个椭圆的面积,
同理可得${∫}_{0}^{3}$$\sqrt{3-\frac{1}{3}{x}^{2}}$dx表示椭圆$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{3}$=1的四分之一个椭圆的面积,
故${∫}_{0}^{3}$$\sqrt{5-\frac{5}{9}{x}^{2}}$dx>${∫}_{0}^{3}$$\sqrt{3-\frac{1}{3}{x}^{2}}$dx
点评 本题考查定积分的几何意义,涉及椭圆的知识,属基础题.

练习册系列答案
相关题目
2.直线l与平面α垂直的一个充分条件是( )
| A. | l垂直于平面α内的一条直线 | B. | l垂直于平面α内的两条直线 | ||
| C. | l垂直于平面α内的无数条直线 | D. | l垂直于平面α内的任一条直线 |
6.若$\frac{5π}{2}$<α<3π,则$\sqrt{\frac{1}{2}+\frac{1}{2}\sqrt{\frac{1}{2}+\frac{1}{2}cosα}}$等于( )
| A. | cos$\frac{α}{4}$ | B. | -cos$\frac{α}{4}$ | C. | sin$\frac{α}{4}$ | D. | -sin$\frac{α}{4}$ |
7.已知函数f(x)=4sin(2x+$\frac{π}{6}$),x∈R,则下列命题正确的是( )
| A. | f(x)在区间[0,$\frac{π}{2}$]内是增函数 | |
| B. | 若?x1≠x2,f(x1)=f(x2)=0,则x1-x2必是π的整数倍 | |
| C. | f(x)的图象关于点(-$\frac{π}{12}$+$\frac{kπ}{2}$,0)(k∈Z)对称 | |
| D. | f(x)的图象关于直线x=$\frac{π}{12}$对称 |
 如图,在四边形ABCD中,AB=4,BC=$\frac{3}{2}$,CD=$\frac{5}{2}$,∠A=$\frac{π}{3}$,cos∠ADB=$\frac{1}{7}$.
如图,在四边形ABCD中,AB=4,BC=$\frac{3}{2}$,CD=$\frac{5}{2}$,∠A=$\frac{π}{3}$,cos∠ADB=$\frac{1}{7}$.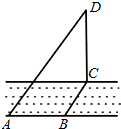 如图,在河的一侧有一塔CD=12m,河宽BC=3m,另一侧有点A,AB=4m,则点A与塔顶D的距离AD=13.
如图,在河的一侧有一塔CD=12m,河宽BC=3m,另一侧有点A,AB=4m,则点A与塔顶D的距离AD=13.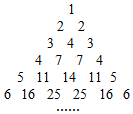 如图三角形数阵满足:
如图三角形数阵满足: