题目内容
3.△ABC中,角A,B,C的对边分别为a,b,c,且满足bcosA=(2c+a)cos(C+A)•(I)求角B的大小;
( II)若b=4,△ABC的面积为$\sqrt{3}$,求a+c的值.
分析 (I)由正弦定理,两角和的正弦函数公式,三角形内角和定理,诱导公式化简已知可得sinC=-2sinCcosB,结合sinC>0,可求cosB的值,结合B的范围即可得解B的值.
( II)由三角形面积公式可求ac的值,由余弦定理即可得解a+c的值.
解答 (本小题满分12分)
解:(I)由条件,得bcosA=(2c+a)cos(π-B)=-(2c+a)cosB,…(1分)
由正弦定理,得sinBcosA=-(2sinC+sinA)cosB,…(3分)
即sinAcosB+cosAsinB=-2sinCcosB,
即sin(A+B)=-2sinCcosB.…(4分)
∵sin(A+B)=sin(π-C)=sinC>0,
∴$cosB=-\frac{1}{2}$…(5分)
∵B∈(0,π),
∴$B=\frac{2π}{3}•$…(6分)
( II)由(I)知$B=\frac{2π}{3}$,则${S_{△ABC}}=\frac{1}{2}acsin\frac{2π}{3}=\sqrt{3}$.
得ac=4.…(8分)
由余弦定理,得${b^2}={a^2}+{c^2}-2accos\frac{2π}{3}={a^2}+{c^2}+ac={(a+c)^2}-ac={(a+c)^2}-4$.…(10分)
∵b=4,
∴(a+c)2=20.故$a+c=2\sqrt{5}$.…(12分)
点评 本题主要考查了正弦定理,两角和的正弦函数公式,三角形内角和定理,诱导公式,三角形面积公式,余弦定理在解三角形中的应用,考查了转化思想,属于中档题.

练习册系列答案
相关题目
11.已知△ABC是锐角三角形,若A=2B,则$\frac{a}{b}$的取值范围是( )
| A. | ($\sqrt{2}$,$\sqrt{3}$) | B. | ($\sqrt{2}$,2) | C. | (1,$\sqrt{3}$) | D. | (1,2) |
18.曲线f(x)=-x3+3x2在点(1,f(1))处的切线截圆x2+(y+1)2=4所得弦长为( )
| A. | 4 | B. | 2$\sqrt{2}$ | C. | 2 | D. | $\sqrt{2}$ |
8.《九章算术》是我国古代内容极为丰富的一部数学专著,书中有如下问题:今有女子善织,日增等尺,七日织28尺,第二日,第五日,第八日所织之和为15尺,则第九日所织尺数为( )
| A. | 8 | B. | 9 | C. | 10 | D. | 11 |
13.如图,小方格是边长为1的正方形,一个几何体的三视图如图,则几何体的表面积为( )
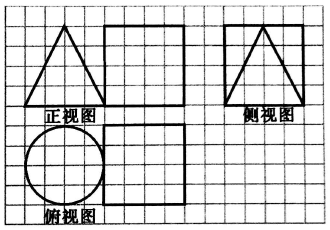

| A. | 4$\sqrt{5}π+96$ | B. | (2$\sqrt{5}+6$)π+96 | C. | (4$\sqrt{5}+4$)π+64 | D. | (4$\sqrt{5}$+4)π+96 |
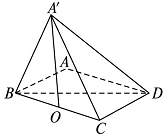 如图,矩形ABCD中,AB=2,BC=4,将△ABD沿对角线BD折起到△A′BD的位置,使点A′在平面BCD内的射影点O恰好落在BC边上,则异面直线A′B与CD所成角的大小为90°.
如图,矩形ABCD中,AB=2,BC=4,将△ABD沿对角线BD折起到△A′BD的位置,使点A′在平面BCD内的射影点O恰好落在BC边上,则异面直线A′B与CD所成角的大小为90°.