题目内容
4.已知数列{an}中a1=1,an=$\frac{1}{2}$an-1+1(n≥2),则an=( )| A. | 2-($\frac{1}{2}$)n-1 | B. | ($\frac{1}{2}$)n-1-2 | C. | 2-2n-1 | D. | 2n-1 |
分析 an=$\frac{1}{2}$an-1+1(n≥2),变形为an-2=$\frac{1}{2}$(an-1-2),利用等比数列的通项公式即可得出.
解答 解:∵an=$\frac{1}{2}$an-1+1(n≥2),∴an-2=$\frac{1}{2}$(an-1-2),又a1-2=-1.
∴数列{an-2}是等比数列,首项为-1,公比为$\frac{1}{2}$.
∴an-2=-1×$(\frac{1}{2})^{n-1}$,即an=2-$(\frac{1}{2})^{n-1}$,
故选:A.
点评 本题考查了数列的递推关系、等比数列的通项公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
19.△ABC的三边长分别为|AB|=7,|BC|=5,|CA|=6,则$\overrightarrow{AB}$•$\overrightarrow{BC}$ 的值为( )
| A. | 19 | B. | 14 | C. | -18 | D. | -19 |
16.已知函数f(x)=2x,等差数列{an}的公差为2.若f(a2+a4+a6+a8+a10)=4,则log2[f(a1)•f(a2)•f(a3)•…•f(a10)]=( )
| A. | 8 | B. | 4 | C. | -6 | D. | $\frac{1}{4}$ |
13.如图,小方格是边长为1的正方形,一个几何体的三视图如图,则几何体的表面积为( )
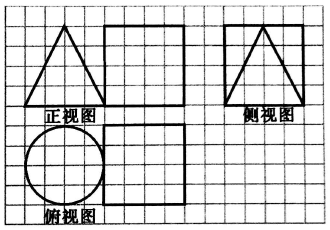

| A. | 4$\sqrt{5}π+96$ | B. | (2$\sqrt{5}+6$)π+96 | C. | (4$\sqrt{5}+4$)π+64 | D. | (4$\sqrt{5}$+4)π+96 |
14.已知数列{an}的前n项和为Sn,a1=1,an+1=3Sn+2,则a4=( )
| A. | 64 | B. | 80 | C. | 256 | D. | 320 |
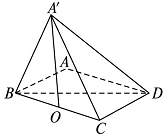 如图,矩形ABCD中,AB=2,BC=4,将△ABD沿对角线BD折起到△A′BD的位置,使点A′在平面BCD内的射影点O恰好落在BC边上,则异面直线A′B与CD所成角的大小为90°.
如图,矩形ABCD中,AB=2,BC=4,将△ABD沿对角线BD折起到△A′BD的位置,使点A′在平面BCD内的射影点O恰好落在BC边上,则异面直线A′B与CD所成角的大小为90°.