题目内容
2.在△ABC中,若$\overrightarrow{AB}$•$\overrightarrow{AC}$=5且|$\overrightarrow{AB}$-$\overrightarrow{AC}$|=4,则△ABC面积的最大值为( )| A. | 6 | B. | $\frac{15}{2}$ | C. | 10 | D. | 12 |
分析 设A、B、C所对边分别为a,b,c,由$\overrightarrow{AB}$•$\overrightarrow{AC}$=5且|$\overrightarrow{AB}$-$\overrightarrow{AC}$|=4,得bccosA=5,a=4,结合余弦定理可得b2+c2,再由基本不等式可得bc最大值,即可求出△ABC面积的最大值.
解答 解:设A、B、C所对边分别为a,b,c,
由$\overrightarrow{AB}$•$\overrightarrow{AC}$=5,|$\overrightarrow{AB}$-$\overrightarrow{AC}$|=4,得bccosA=5,a=4,①
S△ABC=$\frac{1}{2}$bcsinA=$\frac{1}{2}$bc$\sqrt{1-co{s}^{2}A}$=$\frac{1}{2}$bc$•\sqrt{1-\frac{25}{{b}^{2}{c}^{2}}}$=$\frac{1}{2}\sqrt{{b}^{2}{c}^{2}-25}$,
由余弦定理可得b2+c2-2bccosA=16,②
由①②消掉cosA得b2+c2=26,
∴bc≤$\frac{{b}^{2}+{c}^{2}}{2}$=13,当且仅当b=c=$\frac{13}{2}$时取等号,
∴S△ABC=$\frac{1}{2}$$\sqrt{{b}^{2}{c}^{2}-25}$≤6,
∴△ABC的面积的最大值为6.
故选:A.
点评 本题考查平面向量数量积的运算、三角形面积公式、基本不等式求最值等知识,综合性较强,属中档题.

练习册系列答案
相关题目
13.如图,小方格是边长为1的正方形,一个几何体的三视图如图,则几何体的表面积为( )
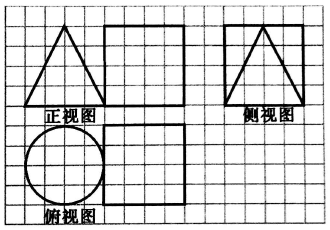

| A. | 4$\sqrt{5}π+96$ | B. | (2$\sqrt{5}+6$)π+96 | C. | (4$\sqrt{5}+4$)π+64 | D. | (4$\sqrt{5}$+4)π+96 |
10.设{an}是首项为a1,公比为q的等比数列,则“a1q>0”是“{an}为递增数列”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
17.已知公差不为0的等差数列{an}满足a1,a3,a4成等比数列,Sn为数列{an}的前n项和,则$\frac{{{S_4}-{S_2}}}{{{S_5}-{S_3}}}$的值为( )
| A. | -2 | B. | -3 | C. | 2 | D. | 3 |
14.已知数列{an}的前n项和为Sn,a1=1,an+1=3Sn+2,则a4=( )
| A. | 64 | B. | 80 | C. | 256 | D. | 320 |