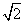Question

自圆O外一点P引圆的切线，切点为A，M为PA的中点，过M引圆的割线交圆于B，C两点，且∠BMP＝100°，∠BPC＝40°，则∠MPB的大小为(　　)

A．10°　　　B．20°　　　C．30°　　　D．40°

Answer 1

B

[解析]　因为PA与圆相切于点A，所以AM²＝MB·MC.而M为PA的中点，

所以PM＝MA，则PM²＝MB·MC，∴＝.

又∠BMP＝∠PMC，所以ΔBMP∽△PMC，所以∠MPB＝∠MCP，在△PMC中，由∠CMP＋∠MPC＋∠MCP＝180°，

即∠CMP＋∠BPC＋2∠MPB＝180°，所以100°＋40°＋2∠MPB＝180°，从而∠MPB＝20°.