题目内容
用数学归纳法证明“n3＋(n＋1)3＋(n＋2)3(n∈N＋)能被9整除”，要利用归纳假设证n＝k＋1时的情况，只需展开( )
A．(k＋3)3 B．(k＋2)3
C．(k＋1)3 D．(k＋1)3＋(k＋2)3
A
[解析] 假设当n＝k时，原式能被9整除，即k3＋(k＋1)3＋(k＋2)3能被9整除．
当n＝k＋1时，(k＋1)3＋(k＋2)3＋(k＋3)3为了能用上面的归纳假设，只需将(k＋3)3展开，让其出现k3即可．
练习册系列答案
相关题目
＋
＋
，则
的最大值为________．
≥2
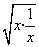＝2，x＋
＝
＋
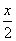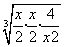＝3，…，我们可以得出推广结论：x＋
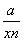≥n＋1(n∈N＋)，则a＝( )
＋
＋…＋
>
(n∈N＋)成立，其初始值至少应取( )
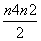，则当n＝k＋1时左端应在n＝k的基础上加上( )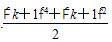
(ρ∈R)和ρcosθ＝2
＝1，过定点P(2,1)作直线交双曲线于P1，P2两点，并使P(2,1)为P1P2的中点，则此直线方程是________．