题目内容
1.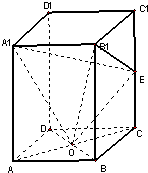 长方体ABCD-A1B1C1D1中,AB=BC=4,AA1=8,E是CC1的中点,O是下底面正方形ABCD的中心.
长方体ABCD-A1B1C1D1中,AB=BC=4,AA1=8,E是CC1的中点,O是下底面正方形ABCD的中心.(1)求二面角C1-A1B1-O的大小(结果用反三角函数值表示)
(2)求异面直线A1B1与EO所成角的大小(结果用反三角函数值表示)
分析 (1)以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,利用向量法能求出二面角C1-A1B1-O的大小.
(2)求出$\overrightarrow{{A}_{1}{B}_{1}}$=(0,4,0),$\overrightarrow{EO}$=(2,-2,-4),利用向量法能求出异面直线A1B1与EO所成角的大小.
解答 解: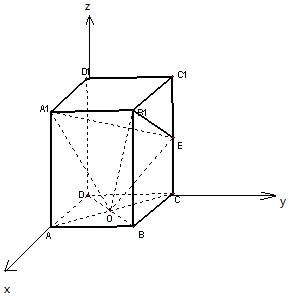 (1)以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,
(1)以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,
则O(2,2,0),A1(4,0,8),B1(4,4,8),
$\overrightarrow{O{A}_{1}}$=(2,-2,8),$\overrightarrow{O{B}_{1}}$=(2,2,8),
设平面A1B1O的法向量$\overrightarrow{n}$=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{O{A}_{1}}=2x-2y+8z=0}\\{\overrightarrow{n}•\overrightarrow{O{B}_{1}}=2x+2y+8z=0}\end{array}\right.$,取z=1,得$\overrightarrow{n}$=(-4,0,1),
平面A1B1C1的法向量$\overrightarrow{m}$=(0,0,1),
设二面角C1-A1B1-O的平面角为θ,
则cosθ=$\frac{|\overrightarrow{m}•\overrightarrow{n}|}{|\overrightarrow{m}|•|\overrightarrow{n}|}$=$\frac{1}{\sqrt{17}}$=$\frac{\sqrt{17}}{17}$,
∴θ=arccos$\frac{\sqrt{17}}{17}$.
∴二面角C1-A1B1-O的大小为arccos$\frac{\sqrt{17}}{17}$.
(2)E(0,4,4),$\overrightarrow{{A}_{1}{B}_{1}}$=(0,4,0),$\overrightarrow{EO}$=(2,-2,-4),
设异面直线A1B1与EO所成角为α,
则cosα=$\frac{|\overrightarrow{{A}_{1}{B}_{1}}•\overrightarrow{EO}|}{|\overrightarrow{{A}_{1}{B}_{1}}|•|\overrightarrow{EO}|}$=$\frac{8}{4\sqrt{24}}$=$\frac{\sqrt{6}}{6}$,
∴$θ=arccos\frac{\sqrt{6}}{6}$.
∴异面直线A1B1与EO所成角的大小为arccos$\frac{\sqrt{6}}{6}$.
点评 本题考查二面角的大小的求法,考查异面直线所成角的大小的求法,是中档题,解题时要认真审题,注意向量法的合理运用.

 名校通行证有效作业系列答案
名校通行证有效作业系列答案| A. | n+1 | B. | n | C. | n-1 | D. | n-2 |
| X | 0 | 1 | 2 | 3 |
| P | $\frac{1}{8}$ | $\frac{3}{8}$ | $\frac{3}{8}$ | a |
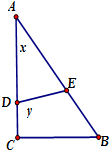 如图,在直角三角形ABC中,∠ACB=90°,AC=4,BC=3,点D,E分别线段AC,AB上,线段DE分三角形ABC为面积相等的两部分,设AD=x,DE=y.
如图,在直角三角形ABC中,∠ACB=90°,AC=4,BC=3,点D,E分别线段AC,AB上,线段DE分三角形ABC为面积相等的两部分,设AD=x,DE=y.