题目内容
17.过抛物线y2=4x的焦点作直线交抛物线于A,B两点,若O为坐标原点,则$\overrightarrow{OA}$•$\overrightarrow{OB}$=( )| A. | -1 | B. | -2 | C. | -3 | D. | -4 |
分析 由抛物线y2=4x与过其焦点(1,0)的直线方程联立,消去y整理成关于x的一元二次方程,设出A(x1,y1)、B(x2,y2)两点坐标,则$\overrightarrow{OA}$•$\overrightarrow{OB}$=x1•x2+y1•y2,由韦达定理可以求得答案.
解答 解:由题意知,抛物线y2=4x的焦点坐标为(1,0),∴直线AB的方程为y=k(x-1),
由$\left\{\begin{array}{l}{y=k(x-1)}\\{{y}^{2}=4x}\end{array}\right.$,得k2x2-(2k2+4)x+k2=0,设A(x1,y1),B(x2,y2),
x1+x2=$\frac{2{k}^{2}+4}{{k}^{2}}$,x1+x2=1,y1•y2=k(x1-1)•k(x2-1)=k2[x1•x2-(x1+x2)+1]'
则$\overrightarrow{OA}$•$\overrightarrow{OB}$=x1•x2+y1•y2=x1•x2+k(x1-1)•k(x2-1)=-3.
故选:C.
点评 题考查直线与圆锥曲线的关系,解决问题的关键是联立抛物线方程与过其焦点的直线方程,利用韦达定理予以解决,属于基础题.

练习册系列答案
相关题目
8.已知定义在R上的奇函数f(x)满足:当x≥0时,f(x)=x3,若不等式f(-4t)>f(2m+mt2)对任意实数t恒成立,则实数m的取值范围是( )
| A. | (-∞,-$\sqrt{2}$) | B. | (-$\sqrt{2}$,0) | C. | (-∞,0)∪($\sqrt{2}$,+∞) | D. | (-∞,-$\sqrt{2}$)∪($\sqrt{2}$,+∞) |
5.在(x-2)10展开式中,二项式系数的最大值为 a,含x7项的系数为b,则$\frac{b}{a}$=( )
| A. | $\frac{80}{21}$ | B. | $\frac{21}{80}$ | C. | $-\frac{21}{80}$ | D. | $-\frac{80}{21}$ |
12.在△ABC中,若a=1,b=2,cosA=$\frac{2\sqrt{2}}{3}$,则sinB=( )
| A. | $\frac{\sqrt{2}}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{\sqrt{2}}{3}$ | D. | $\frac{2}{3}$ |
2.若x,y满足$\left\{\begin{array}{l}{x≤y≤2x}\\{x+y≤1}\end{array}\right.$,则z=x+2y的取值范围为[0,$\frac{5}{3}$].
9.已知直线ax+2y+2=0与3x-y-2=0平行,则系数a=( )
| A. | 3 | B. | -6 | C. | -$\frac{3}{2}$ | D. | $\frac{2}{3}$ |
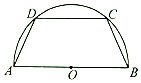 如图,有一块半径为2的半圆形钢板,计划剪裁成等腰梯形ABCD的形状,它的下底AB是⊙O的直径,上底CD的端点在圆周上.设∠DAB=θ(0<θ<$\frac{π}{2}$),L为等腰梯形ABCD的周长.
如图,有一块半径为2的半圆形钢板,计划剪裁成等腰梯形ABCD的形状,它的下底AB是⊙O的直径,上底CD的端点在圆周上.设∠DAB=θ(0<θ<$\frac{π}{2}$),L为等腰梯形ABCD的周长.