题目内容
2.若x,y满足$\left\{\begin{array}{l}{x≤y≤2x}\\{x+y≤1}\end{array}\right.$,则z=x+2y的取值范围为[0,$\frac{5}{3}$].分析 画出约束条件的可行域,利用目标函数的几何意义,求解范围即可.
解答 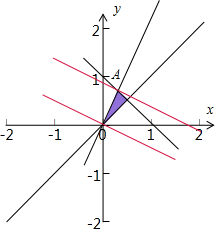 解:x,y满足$\left\{\begin{array}{l}{x≤y≤2x}\\{x+y≤1}\end{array}\right.$,不是的可行域如图:
解:x,y满足$\left\{\begin{array}{l}{x≤y≤2x}\\{x+y≤1}\end{array}\right.$,不是的可行域如图:
z=x+2y化为:y=-$\frac{1}{2}x$+$\frac{1}{2}z$,当y=-$\frac{1}{2}x$+$\frac{1}{2}z$经过可行域的O时
目标函数取得最小值,经过A时,目标函数取得最大值,
由$\left\{\begin{array}{l}{x+y=1}\\{y=2x}\end{array}\right.$,可得A($\frac{1}{3}$,$\frac{2}{3}$),
则z=x+2y的最小值为:0;最大值为:$\frac{1}{3}+2×\frac{2}{3}$=$\frac{5}{3}$.
则z=x+2y的取值范围为:[0,$\frac{5}{3}$].
故答案为:[0,$\frac{5}{3}$].
点评 本题考查的知识点是简单线性规划的应用,其中利用角点法是解答线性规划类小题最常用的方法,一定要掌握.

练习册系列答案
相关题目
12.已知△ABC是钝角三角形,若AC=1,BC=2,且△ABC的面积为$\frac{{\sqrt{3}}}{2}$,则AB=( )
| A. | $\sqrt{3}$ | B. | $\sqrt{7}$ | C. | $2\sqrt{2}$ | D. | 3 |
13.图中的三个直角三角形是一个体积为20cm3几何体的三视图,则h=( )
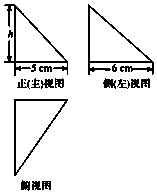

| A. | 4 | B. | 5 | C. | 6 | D. | 3 |
10.不等式$\frac{1}{x}$>1的解集为( )
| A. | (-∞,1) | B. | (0,1) | C. | (1,+∞) | D. | (0,+∞) |
17.过抛物线y2=4x的焦点作直线交抛物线于A,B两点,若O为坐标原点,则$\overrightarrow{OA}$•$\overrightarrow{OB}$=( )
| A. | -1 | B. | -2 | C. | -3 | D. | -4 |
12.若3m=b,则${log_{3^2}}b$=( )
| A. | 2m | B. | $\frac{m}{2}$ | C. | m2 | D. | $\sqrt{m}$ |
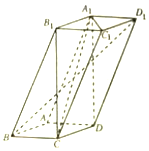 如图,四棱柱ABCD-A1B1C1D1中,A1D⊥平面ABCD,底面为边长为1的正方形,侧棱AA1=2
如图,四棱柱ABCD-A1B1C1D1中,A1D⊥平面ABCD,底面为边长为1的正方形,侧棱AA1=2