题目内容
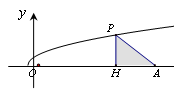
如图,已知点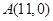 ,直线
,直线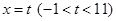 与函数
与函数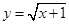 的图象交于点
的图象交于点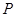 ,与
,与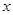 轴交于点
轴交于点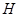 ,记
,记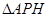 的面积为
的面积为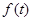 .
.
(Ⅰ)求函数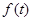 的解析式;
的解析式;
(Ⅱ)求函数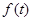 的最大值.
的最大值.
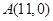 ,直线
,直线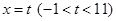 与函数
与函数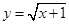 的图象交于点
的图象交于点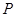 ,与
,与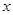 轴交于点
轴交于点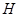 ,记
,记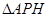 的面积为
的面积为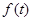 .
.
(Ⅰ)求函数
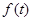 的解析式;
的解析式;(Ⅱ)求函数
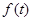 的最大值.
的最大值.(Ⅰ) . (Ⅱ)
. (Ⅱ)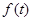 最大值为8.
最大值为8.
 . (Ⅱ)
. (Ⅱ)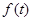 最大值为8.
最大值为8. 试题分析:(Ⅰ)确定三角形面积,主要确定底和高
 .
.(Ⅱ)应用导数研究函数的最值,遵循“求导数,求驻点,讨论驻点两侧导数正负,比较极值与区间端点函数值”.利用“表解法”形象直观,易以理解.
试题解析:(Ⅰ)由已知
 1分
1分所以
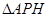 的面积为
的面积为 . 4分
. 4分(Ⅱ)解法1.

 7分
7分由
 得
得 , 8分
, 8分函数
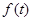 与
与 在定义域上的情况下表:
在定义域上的情况下表: |  | 3 |  |
 | + | 0 |  |
 | ↗ | 极大值 | ↘ |
所以当
 时,函数
时,函数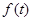 取得最大值8. 13分
取得最大值8. 13分解法2.由

设
 , 6分
, 6分则
 . 7分
. 7分函数
 与
与 在定义域上的情况下表:
在定义域上的情况下表: |  | 3 |  |
 | + | 0 |  |
 | ↗ | 极大值 | ↘ |
所以当
 时,函数
时,函数 取得最大值, 12分
取得最大值, 12分所以当
 时,函数
时,函数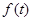 取得最大值
取得最大值 . 13分
. 13分
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
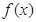 =
=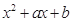 ,
,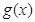 =
=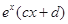 ,若曲线
,若曲线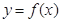 和曲线
和曲线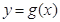 都过点P(0,2),且在点P处有相同的切线
都过点P(0,2),且在点P处有相同的切线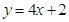 .
.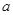 ,
,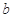 ,
,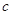 ,
,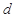 的值;
的值;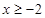 时,
时,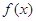 ≤
≤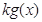 ,求
,求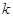 的取值范围.
的取值范围.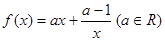 ,
,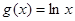 .
.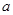 ,函数
,函数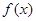 与
与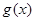 的图象在
的图象在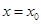 处的切线斜率总相等,求
处的切线斜率总相等,求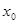 的值;
的值;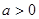 ,对任意
,对任意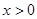 ,不等式
,不等式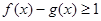 恒成立,求实数
恒成立,求实数 ,
, 的单调性;
的单调性; .
.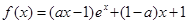 .
. 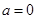 ,
,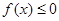 ;
;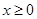 时,
时,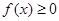 ,求
,求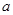 的取值范围.
的取值范围.  .
. 为奇函数,求a的值;
为奇函数,求a的值; 在
在 处取得极大值,求实数a的值;
处取得极大值,求实数a的值; ,求
,求 上的最大值.
上的最大值. .
.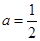 ,求函数
,求函数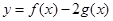 的极值,
的极值, ,使得
,使得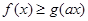 成立?若存在,求出实数
成立?若存在,求出实数 所表示的平面区域为D,直线
所表示的平面区域为D,直线 与D有公共点,则
与D有公共点,则 的取值范围是________
的取值范围是________ ,其导函数记为
,其导函数记为 ,则
,则
 .
.