题目内容
18.已知椭圆E过点A(2,3),对称轴为坐标轴,焦点F1,F2在x轴上,离心率e=$\frac{1}{2}$,∠F1AF2的平分线所在直线为l.(Ⅰ)求椭圆E的方程;
(Ⅱ)设l与x轴的交点为Q,求点Q的坐标及直线l的方程;
(Ⅲ)在椭圆E上是否存在关于直线l对称的相异两点?若存在,请找出;若不存在,说明理由.
分析 (Ⅰ)设出椭圆方程,根据椭圆E经过点A(2,3),离心率,建立方程组,求得几何量,即可得到椭圆E的方程;
(Ⅱ)求得AF1方程、AF2方程,利用角平分线性质,即可求得∠F1AF2的平分线所在直线l的方程;
(Ⅲ)假设存在B(x1,y1)C(x2,y2)两点关于直线l对称,设出直线BC方程代入椭圆E的方程,求得BC中点代入直线2x-y-1=0上,即可得到结论.
解答 解:(Ⅰ)设椭圆方程为$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$ (a>b>0)
∵椭圆E经过点A(2,3),离心率e=$\frac{1}{2}$,
∴$\left\{\begin{array}{l}{\frac{c}{a}=\frac{1}{2}}\\{\frac{4}{{a}^{2}}+\frac{9}{{b}^{2}}=1}\\{{a}^{2}={b}^{2}+{c}^{2}}\end{array}\right.$解a2=16,b2=12.
∴椭圆方程E为:$\frac{{x}^{2}}{16}+\frac{{y}^{2}}{12}=1$.
(Ⅱ)F1(-2,0),F2(2,0),
∵A(2,3),∴AF1方程为:3x-4y+6=0,AF2方程为:x=2
设角平分线上任意一点为P(x,y),$\frac{|3x-4y+6|\\;\\;}{5}=|\\;x-2|\$;
得2x-y-1=0或x+2y-8=0
∵斜率为正,∴直线方程为2x-y-1=0;l与x轴的交点为Q,点Q的坐标($\frac{1}{2}$,0).
(Ⅲ)假设存在B(x1,y1)C(x2,y2)两点关于直线l对称,∴kBC=-$\frac{1}{2}$,
∴直线BC方程为y=-$\frac{1}{2}$x+m代入椭圆方程$\frac{{x}^{2}}{16}+\frac{{y}^{2}}{12}=1$.,
得x2-mx+m2-12=0,∴BC中点为($\frac{m}{2},\frac{3m}{4}$)
代入直线2x-y-1=0上,得m=4.
∴BC中点为(2,3)与A重合,不成立,所以不存在满足题设条件的相异的两点.
点评 本题考查椭圆的标准方程,考查直线方程,考查对称性,考查学生分析解决问题的能力,属于中档题.

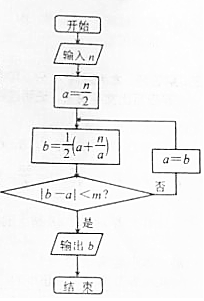 一种在实数域和复数域上近似求解方程的方法可以设计如图所示的程序框图,若输入的n为6时,输出结果为2.45,则m可以是( )
一种在实数域和复数域上近似求解方程的方法可以设计如图所示的程序框图,若输入的n为6时,输出结果为2.45,则m可以是( )| A. | 0.6 | B. | 0.1 | C. | 0.01 | D. | 0.05 |
| A. | -2 | B. | -1 | C. | 2 | D. | 1 |
| A. | [-1,2) | B. | [-1,1] | C. | (0,1] | D. | (-∞,2) |
| A. | 等腰直角三角形 | B. | 等边三角形 | ||
| C. | 直角非等腰三角形 | D. | 等腰非直角三角形 |