题目内容
11．复数z=$\frac{{m}^{2}+m-6}{m}$+（m2-2m）i为纯虚数，m=-3．分析 根据纯虚数的定义得到关于m的不等式组，解出即可．
解答 解：若复数z是纯虚数，
则$\left\{\begin{array}{l}{\frac{{m}^{2}+m-6}{m}=0}\\{{m}^{2}-2m≠0}\end{array}\right.$，解得：m=-3，
故答案为：-3．
点评 本题考查了纯虚数的定义，考查不等式问题，是一道基础题．
练习册系列答案
相关题目
1．函数$y=sin（2x+\frac{π}{3}）$图象中的一条对称轴的方程是（ ）
| A． | $x=\frac{π}{12}$ | B． | $x=\frac{π}{6}$ | C． | $x=\frac{π}{3}$ | D． | $x=-\frac{π}{12}$ |
6．如图，小正方形的边长为1，粗线画出的是某几何体的三视图，则该几何体的体积为（ ）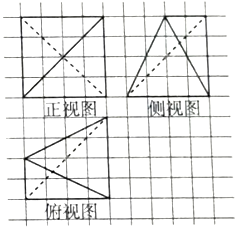
| A． | 8$\sqrt{3}$ | B． | $\frac{80}{3}$ | C． | 16$\sqrt{3}$ | D． | 32 |