题目内容
17.在平面直角坐标系xOy中,以点(2,1)为圆心且与直线mx+y-2m=0(m∈R)相切的所有圆中,半径最大的圆的标准方程为(x-2)2+(y-1)2=1.分析 由题意画出图形,得到以点(2,1)为圆心且与直线mx+y-2m=0(m∈R)相切的所有圆的半径的最大值,则答案可求.
解答  解:如图,
解:如图,
直线mx+y-2m=0过定点(2,0),
则以点(2,1)为圆心且与直线mx+y-2m=0(m∈R)相切的所有圆中,
半径的最大值为1,
∴半径最大的圆的标准方程为(x-2)2+(y-1)2=1.
故答案为:(x-2)2+(y-1)2=1.
点评 本题考查圆的标准方程,考查了数形结合的解题思想方法,是基础题.

练习册系列答案
相关题目
7.按顺序输入x,y,z的值,运行如图的程序后,输出的结果为8,则输入的x,y,z的值可能是( )
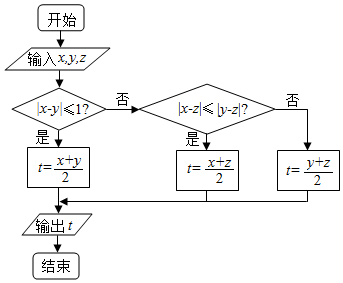

| A. | x=6,y=8,z=9 | B. | x=8,y=7,z=9 | C. | x=8,y=6,z=10 | D. | x=8,y=6,z=8 |
8.已知函数f(x)=x3-x2-x+a的图象与x轴只有一个交点,则实数a的取值范围是( )
| A. | (-∞,-1)∪(-$\frac{1}{9}$,+∞) | B. | (-$\frac{5}{27}$,1) | C. | (-∞,1) | D. | (-∞,-$\frac{5}{27}$)∪(1,+∞) |
5.已知函数f(x)=cos2x+asinx在区间(0,nπ)内恰有8个零点,则实数a的取值范围与最小正整数n的值分别为( )
| A. | (-1,1),2 | B. | (-1,1),4 | C. | [-1,1],2 | D. | [-1,1],4 |
3.已知集合M={x|0<x<2},N={x|x>1},则M∩N=( )
| A. | [1,2) | B. | (1,2) | C. | [0,1) | D. | (0,1] |