题目内容
15.已知向量$\overrightarrow a=(1,m)$,$\overrightarrow b=(-1,2m+1)$,且$\overrightarrow a∥\overrightarrow b$,则m=-$\frac{1}{3}$.分析 利用向量平行的性质直接求解.
解答 解:∵向量$\overrightarrow a=(1,m)$,$\overrightarrow b=(-1,2m+1)$,且$\overrightarrow a∥\overrightarrow b$,
∴$\frac{1}{-1}=\frac{m}{2m+1}$,
解得m=-$\frac{1}{3}$.
故答案为:$-\frac{1}{3}$.
点评 本题考查实数值的求不地,是基础题,解题时要认真审题,注意向量平行的性质的合理运用.

练习册系列答案
相关题目
15.已知a∈R,命题“?x∈(0,+∞),等式lnx=a成立”的否定形式是( )
| A. | ?x∈(0,+∞),等式lnx=a不成立 | B. | ?x∈(-∞,0),等式lnx=a不成立 | ||
| C. | ?x0∈(0,+∞),等式lnx0=a不成立 | D. | ?x0∈(-∞,0),等式lnx0=a不成立 |
3.已知抛物线y2=2px(p>0)上一点M到焦点F的距离等于3p,则直线MF的斜率为( )
| A. | ±$\sqrt{5}$ | B. | ±1 | C. | +$\frac{5}{2}$ | D. | ±$\frac{\sqrt{5}}{2}$ |
20.过点C(2,-1)且与直线x+y-3=0垂直的直线是( )
| A. | x+y-1=0 | B. | x+y+1=0 | C. | x-y-3=0 | D. | x-y-1=0 |
4.在公差为d的等差数列{an}中,“d>1”是“{an}是递增数列”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
 如图,在四棱锥P-ABCD中,底面ABCD为矩形,平面PCD⊥平面ABCD,BC=1,AB=2,$PC=PD=\sqrt{2}$,E为PA中点.
如图,在四棱锥P-ABCD中,底面ABCD为矩形,平面PCD⊥平面ABCD,BC=1,AB=2,$PC=PD=\sqrt{2}$,E为PA中点.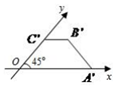 一直角梯形的直观图是一个如图所示的梯形,且OA′=2,B′C′=OC′=1,则该直角梯形的面积为( )
一直角梯形的直观图是一个如图所示的梯形,且OA′=2,B′C′=OC′=1,则该直角梯形的面积为( )