题目内容
某农户计划种植黄瓜和韭菜,种植面积不超过50亩,投入资金54万元,佛山市种植黄瓜和韭菜的产量,成本和售价如下:
为使一年的种植总利润(总利润=总销售收入-总种植成本)最大,那么黄瓜种植面积应为 亩.
| 年产量亩 | 年种植成本 | 每吨售价 | |
| 黄瓜 | 4吨 | 1.2万元 | 0.55万元 |
| 韭菜 | 6吨 | 0.9万元 | 0.3万元 |
考点:简单线性规划的应用
专题:
分析:根据条件,设黄瓜和韭菜的种植面积分别为x,y亩,总利润为z万元,建立目标函数和约束条件,根据线性规划的知识求最优解即可.
解答:
解:设黄瓜和韭菜的种植面积分别为x,y亩,总利润为z万元,
则目标函数为z=(0.55×4x-1.2x)+(0.3×6y-0.9y)=x+0.9y.
线性约束条件为
,
即
,作出不等式组
表示的可行域,
易求得点 A(0,50),B(30,20),C(0,45).
平移直线z=x+0.9y,可知当直线z=x+0.9y 经过点B(30,20),即x=30,y=20时,z取得最大值,且Zmax=48(万元).
故黄瓜和韭菜的种植面积应该分别是30亩、20亩时,利润最大
故黄瓜种植面积为30亩,
故答案为:30.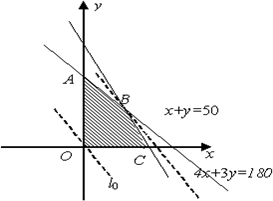
则目标函数为z=(0.55×4x-1.2x)+(0.3×6y-0.9y)=x+0.9y.
线性约束条件为
|
即
|
|
易求得点 A(0,50),B(30,20),C(0,45).
平移直线z=x+0.9y,可知当直线z=x+0.9y 经过点B(30,20),即x=30,y=20时,z取得最大值,且Zmax=48(万元).
故黄瓜和韭菜的种植面积应该分别是30亩、20亩时,利润最大
故黄瓜种植面积为30亩,
故答案为:30.

点评:本题主要考查生活中的优化问题,利用条件建立二元二次不等式组,利用线性规划的知识进行求解是解决本题的关键.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
不等式x-2y+5>0表示的区域在直线x-2y+5=0的( )
| A、右上方 | B、右下方 |
| C、左上方 | D、左下方 |
 某制造商3月生产了一批乒乓球,随机抽取100个进行检查,测得每个球的直径(单位:mm),将数据分组如下表:
某制造商3月生产了一批乒乓球,随机抽取100个进行检查,测得每个球的直径(单位:mm),将数据分组如下表: 某数学老师对本校2013届高三学生某次联考的数学成绩进行分析,按1:50进行分层抽样抽取20名学生的成绩进行分析,分数用茎叶图记录如图所示(部分数据丢失),得到的频率分布表如下:
某数学老师对本校2013届高三学生某次联考的数学成绩进行分析,按1:50进行分层抽样抽取20名学生的成绩进行分析,分数用茎叶图记录如图所示(部分数据丢失),得到的频率分布表如下: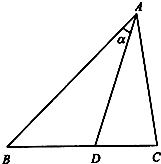 如图,△ABC中,
如图,△ABC中,