题目内容
曲线f（x）=ex在点（x0，f（x0））处的切线经过点P（1，0），则x0= ．
考点：利用导数研究曲线上某点切线方程
专题：导数的综合应用
分析：利用导数的几何意义求切线方程，根据切线过点P，建立方程组求解即可．
解答：
解：曲线的导数为f'（x）=ex，
即切线斜率k=f'（x0）=e x0，
∴在点（x0，f（x0））处的切线方程为y-e x0=e x0（x-x0）．
∵切线经过点P（1，0），
∴-e x0=e x0（1-x0）．
即1-x0=-1，
解得x0=2．
故答案为：2．
即切线斜率k=f'（x0）=e x0，
∴在点（x0，f（x0））处的切线方程为y-e x0=e x0（x-x0）．
∵切线经过点P（1，0），
∴-e x0=e x0（1-x0）．
即1-x0=-1，
解得x0=2．
故答案为：2．
点评：本题主要考查导数的几何意义的应用，利用导数的运算求出切线方程，考查学生的运算能力．
练习册系列答案
精英口算卡系列答案
应用题点拨系列答案
状元及第系列答案
同步奥数系列答案
相关题目
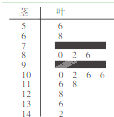某数学老师对本校2013届高三学生某次联考的数学成绩进行分析，按1：50进行分层抽样抽取20名学生的成绩进行分析，分数用茎叶图记录如图所示（部分数据丢失），得到的频率分布表如下：若0＜m＜1，则（ ）
| A、logm（1+m）＞logm（1-m） | ||||
| B、logm（1+m）＞0 | ||||
| C、1-m＞（1+m）2 | ||||
D、(1-m)
|
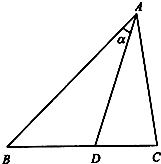如图，△ABC中，