题目内容
有下列说法:
①函数y=-cos2x的最小正周期是π;
②终边在y轴上的角的集合是{a|a=
, k∈Z};
③在同一直角坐标系中,函数y=sinx的图象和函数y=x的图象有三个公共点;
④把函数y=3sin(2x+
)的图象向右平移
个单位长度得到函数y=3sin2x的图象;
⑤函数y=sin(x-
)在[0,π]上是减函数.
其中,正确的说法是 .
①函数y=-cos2x的最小正周期是π;
②终边在y轴上的角的集合是{a|a=
| kπ |
| 2 |
③在同一直角坐标系中,函数y=sinx的图象和函数y=x的图象有三个公共点;
④把函数y=3sin(2x+
| π |
| 3 |
| π |
| 6 |
⑤函数y=sin(x-
| π |
| 2 |
其中,正确的说法是
考点:命题的真假判断与应用
专题:三角函数的图像与性质
分析:①利用周期公式即可求出;
②终边在y轴上的角的集合应是{α|α=kπ+
(k∈Z)}即可判断出;
③令f(x)=x-sinx,则f′(x)=1-cosx≥0,可得函数f(x)在R上单调递增,因此在同一直角坐标系中,函数y=sinx的图象和函数y=x的图象最多有1个公共点;
④把函数y=3sin(2x+
)的图象向右平移
个单位长度得到函数y=3sin[2(x-
)+
],化简即可判断出;
⑤利用诱导公式可得函数y=sin(x-
)=-cosx,再利用余弦函数在[0,π]上的单调性即可.
②终边在y轴上的角的集合应是{α|α=kπ+
| π |
| 2 |
③令f(x)=x-sinx,则f′(x)=1-cosx≥0,可得函数f(x)在R上单调递增,因此在同一直角坐标系中,函数y=sinx的图象和函数y=x的图象最多有1个公共点;
④把函数y=3sin(2x+
| π |
| 3 |
| π |
| 6 |
| π |
| 6 |
| π |
| 3 |
⑤利用诱导公式可得函数y=sin(x-
| π |
| 2 |
解答:
解:①函数y=-cos2x的最小正周期是π,正确;
②终边在y轴上的角的集合是{α|α=kπ+
(k∈Z)}而不是{a|a=
, k∈Z},因此不正确;
③令f(x)=x-sinx,则f′(x)=1-cosx≥0,因此函数f(x)在R上单调递增,而f(0)=0,
可知函数f(x)只有一个零点,x=0.
因此在同一直角坐标系中,函数y=sinx的图象和函数y=x的图象有且仅有1个公共点;
∴③不正确.
④把函数y=3sin(2x+
)的图象向右平移
个单位长度得到函数y=3sin[2(x-
)+
]=3sin2x的图象,z正确;
⑤函数y=sin(x-
)=-cosx,在[0,π]上是增函数,因此不正确.
综上可知:只有①④正确.
故答案为:①④.
②终边在y轴上的角的集合是{α|α=kπ+
| π |
| 2 |
| kπ |
| 2 |
③令f(x)=x-sinx,则f′(x)=1-cosx≥0,因此函数f(x)在R上单调递增,而f(0)=0,
可知函数f(x)只有一个零点,x=0.
因此在同一直角坐标系中,函数y=sinx的图象和函数y=x的图象有且仅有1个公共点;
∴③不正确.
④把函数y=3sin(2x+
| π |
| 3 |
| π |
| 6 |
| π |
| 6 |
| π |
| 3 |
⑤函数y=sin(x-
| π |
| 2 |
综上可知:只有①④正确.
故答案为:①④.
点评:本题考查了三角函数的图象与性质及其变换,属于基础题.

练习册系列答案
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
若平面区域Ω:
的面积为3,则实数k的值为( )
|
A、
| ||
B、
| ||
C、
| ||
D、
|
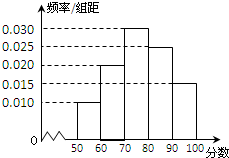 某中学从某次考试成绩中抽取若干名学生的分数,并绘制成如图的频率分布直方图.样本数据分组为[50,60),[60,70),[70,80),[80,90),[90,100].若用分层抽样的方法从样本中抽取分数在[80,100]范围内的数据16个,则其中分数在[90,100]范围内的样本数据有( )
某中学从某次考试成绩中抽取若干名学生的分数,并绘制成如图的频率分布直方图.样本数据分组为[50,60),[60,70),[70,80),[80,90),[90,100].若用分层抽样的方法从样本中抽取分数在[80,100]范围内的数据16个,则其中分数在[90,100]范围内的样本数据有( )