题目内容
若sinα•
+cosα
=-1,则角α的取值范围 .
| sin2α |
| cos2α |
考点:三角函数的化简求值
专题:三角函数的求值
分析:利用平方关系式化简已知条件,然后判断角的范围即可.
解答:
解:sinα•
+cosα
=-1,
可得sinα•|sinα|+cosα|cosα|=-1,
所以
,则α是第三象限角.
即2kπ+π<α<2kπ+
,k∈Z.
故答案为:2kπ+π<α<2kπ+
,k∈Z.
| sin2α |
| cos2α |
可得sinα•|sinα|+cosα|cosα|=-1,
所以
|
即2kπ+π<α<2kπ+
| 3π |
| 2 |
故答案为:2kπ+π<α<2kπ+
| 3π |
| 2 |
点评:本题考查三角函数化简求值,角的范围的求法,考查计算能力.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
已知正项等比数列{an}的公比为q,其前n项积为Tn,并满足a1>1,
<0,则以下结论错误的是( )
| a9a10-1 |
| a9a11-1 |
| A、0<q<1 |
| B、Tn的最大值是T10 |
| C、a9a10>1 |
| D、使Tn>1的最大自然数n为18 |
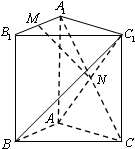 三棱柱ABC-A1B1C1中,侧棱与底面垂直,∠ABC=90°,AB=BC=BB1,M是A1B1的中点,N是AC1与A1C的交点.
三棱柱ABC-A1B1C1中,侧棱与底面垂直,∠ABC=90°,AB=BC=BB1,M是A1B1的中点,N是AC1与A1C的交点.