题目内容
若抛物线y2=8x的顶点是抛物线上到点M（a，0）距离最近的点，则实数a的取值范围是 ．
考点：抛物线的简单性质
专题：圆锥曲线的定义、性质与方程
分析：分类讨论：当a≤0时，满足题意．当a＞0时，设抛物线上任意一点P（x，y），利用两点间的距离公式可得|PM|=
=
=
，再利用二次函数的单调性即可得出．
| (x-a)2+y2 |
| (x-a)2+8x |
| [x-(a-4)]2+8a-16 |
解答：
解：当a≤0时，点M（a，0）是与抛物线上的点距离最近的点．
当a＞0时，设点P（x，y）为抛物线上的任意一点，
则|PM|=
=
=
，
∵当x=0时，上式取得最小值，
∴a-4≤0，解得a≤4，
又a＞0，∴0＜a≤4．
综上可得：实数a的取值范围是（-∞，4]．
故答案为：（-∞，4]．
当a＞0时，设点P（x，y）为抛物线上的任意一点，
则|PM|=
| (x-a)2+y2 |
| (x-a)2+8x |
| [x-(a-4)]2+8a-16 |
∵当x=0时，上式取得最小值，
∴a-4≤0，解得a≤4，
又a＞0，∴0＜a≤4．
综上可得：实数a的取值范围是（-∞，4]．
故答案为：（-∞，4]．
点评：本题考查了二次函数的单调性、分类讨论的思想方法，考查了推理能力和解决问题的能力，属于难题．
练习册系列答案
相关题目
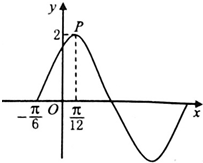已知函数f（x）=2sin（ωx+φ），（ω＞0，φ∈（0，