题目内容
已知数列{an}的通项公式an=
(n∈N+),记f(n)=(1-a1)(1-a2)…(1-an),试通过计算f(1),f(2),f(3)的值,推测出f(n)的值.
| 1 |
| (n+1)2 |
考点:归纳推理,数列的概念及简单表示法
专题:推理和证明
分析:根据数列的通项公式分别计算即可得到结论.
解答:
解:∵f(n)=(1-a1)(1-a2)…(1-an),数列{an}的通项公式an=
,
∴f(1)=1-a1=1-
=
,
f(2)=(1-a1)(1-a2)=f(1)•(1-
)=
•
=
=
,
f(3)=(1-a1)(1-a2)(1-a3)=f(2)•(1-
)=
•
=
.
由此猜想,f(n)=
.
| 1 |
| (n+1)2 |
∴f(1)=1-a1=1-
| 1 |
| 4 |
| 3 |
| 4 |
f(2)=(1-a1)(1-a2)=f(1)•(1-
| 1 |
| 9 |
| 3 |
| 4 |
| 8 |
| 9 |
| 2 |
| 3 |
| 4 |
| 6 |
f(3)=(1-a1)(1-a2)(1-a3)=f(2)•(1-
| 1 |
| 16 |
| 2 |
| 3 |
| 15 |
| 16 |
| 5 |
| 8 |
由此猜想,f(n)=
| n+2 |
| 2(n+1) |
点评:本题主要考查归纳推理的应用,考查学生的计算能力和观察能力.

练习册系列答案
相关题目
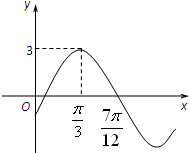 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<