题目内容
8.湛江成功申办2014年广东省第十四届运动会.为做好承办工作,决定选拔3名专业人士加入组委会.经过初选确定4男2女为候选人,每位候选人当选的机会相等.记ξ为女专业人士当选人数.(1)求ξ=0的概率;
(2)求ξ的分布列及Eξ.
分析 (1)利用P(ξ=0)=$\frac{{∁}_{4}^{3}}{{∁}_{6}^{3}}$,即可得出.
(2)ξ的取值为0、1、2.利用P(ξ=k)=$\frac{{∁}_{4}^{3-k}{∁}_{2}^{k}}{{∁}_{6}^{3}}$,即可得出.
解答 解:(1)P(ξ=0)=$\frac{{∁}_{4}^{3}}{{∁}_{6}^{3}}$=$\frac{1}{5}$;
(2)ξ的取值为0、1、2.利用P(ξ=k)=$\frac{{∁}_{4}^{3-k}{∁}_{2}^{k}}{{∁}_{6}^{3}}$.
可得P(ξ=0)=$\frac{1}{5}$,P(ξ=1)=$\frac{3}{5}$,P(ξ=2)=$\frac{1}{5}$.
ξ的分布列为
| ξ | 0 | 1 | 2 |
| P | $\frac{1}{5}$ | $\frac{3}{5}$ | $\frac{1}{5}$ |
点评 本题考查了超几何分布列的概率计算公式及其数学期望,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
20.某校对数学、物理两科进行学业水平考前辅导,辅导后进行测试,按照成绩(满分均为100分)划分为合格(成绩大于或等于70分)和不合格(成绩小于70分).现随机抽取两科各100名学生的成绩统计如下:
(1)试分别估计该校学生数学、物理合格的概率;
(2)设数学合格一人可以赢得4小时机器人操作时间,不合格一人则减少1小时机器人操作时间;物理合格一人可以赢得5小时机器人操作时间,不合格一人则减少2小时机器人操作时间.在(1)的前提下,
(i)记X为数学一人和物理一人共同赢得的机器人操作时间(单位:小时)总和,求随机变量X的分布列和数学期望;
(ii)随机抽取4名学生,求这四名学生物理考前辅导后进行测试所赢得的机器人操作时间不少于13小时的概率.
| 成绩(单位:分) | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
| 数学 | 8 | 12 | 40 | 32 | 8 |
| 物理 | 7 | 18 | 40 | 29 | 6 |
(2)设数学合格一人可以赢得4小时机器人操作时间,不合格一人则减少1小时机器人操作时间;物理合格一人可以赢得5小时机器人操作时间,不合格一人则减少2小时机器人操作时间.在(1)的前提下,
(i)记X为数学一人和物理一人共同赢得的机器人操作时间(单位:小时)总和,求随机变量X的分布列和数学期望;
(ii)随机抽取4名学生,求这四名学生物理考前辅导后进行测试所赢得的机器人操作时间不少于13小时的概率.
16.如图,△AOB为等腰直角三角形,OA=1,OC为斜边AB的高,点P在射线OC上,则$\overrightarrow{AP}•\overrightarrow{OP}$的最小值为( )


| A. | -1 | B. | -$\frac{1}{8}$ | C. | -$\frac{1}{4}$ | D. | -$\frac{1}{2}$ |
 D,同时满足:
D,同时满足: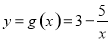 不存在“和谐区间”.
不存在“和谐区间”. (a∈R,a≠0)有“和谐区间”[m,n],当a变化时,求出n﹣m的最大值.
(a∈R,a≠0)有“和谐区间”[m,n],当a变化时,求出n﹣m的最大值. 在一个几何体的三视图中,正视图与俯视图如右图所示,则相应的侧视图可以为( )
在一个几何体的三视图中,正视图与俯视图如右图所示,则相应的侧视图可以为( )



