题目内容
3.设平面直角坐标系的原点为O,直线l的方程为$\left\{\begin{array}{l}{x=2-t}\\{y=\sqrt{3}+t}\end{array}\right.$(t为参数),以O为极点,x轴正方向为极轴正方向建立极坐标系,两坐标系的单位长度相等.动点M(ρ,θ)(ρ>0)且ρ=4cos(θ-$\frac{π}{3}$).(1)求直角坐标系下点M的轨迹C;
(2)求直线l被C截得的线段的长.
分析 (1)利用极坐标与直角坐标的互化方法,求出动点M的直角坐标方程,即可得出直角坐标系下点M的轨迹C;
(2)直线方程化为普通方程,求出圆心到直线的距离,即可求直线l被C截得的线段的长.
解答 解:(1)ρ=4cos(θ-$\frac{π}{3}$),可化为ρ=2cosθ+2$\sqrt{3}$sinθ,
∴ρ2=2ρcosθ+2$\sqrt{3}$ρsinθ,
∴x2+y2=2x+2$\sqrt{3}$y,即(x-1)2+(y-$\sqrt{3}$)2=4,
表示以(1,$\sqrt{3}$)为圆心,2为半径的圆;
(2)直线l的方程为$\left\{\begin{array}{l}{x=2-t}\\{y=\sqrt{3}+t}\end{array}\right.$(t为参数),普通方程为x+y-2-$\sqrt{3}$=0,
圆心到直线的距离d=$\frac{1}{\sqrt{2}}$,
∴直线l被C截得的线段的长=2$\sqrt{4-\frac{1}{2}}$=$\sqrt{14}$.
点评 本题考查极坐标方程、参数方程与直角坐标方程的互化,考查圆心到直线的距离公式,属于中档题.

练习册系列答案
相关题目

 为正相关,
为正相关, 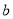 为负相关,
为负相关, 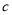 为不相关
为不相关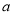 为负相关,
为负相关,  为不相关,
为不相关, 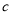 为正相关
为正相关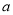 为负相关,
为负相关,  为正相关,
为正相关,  为不相关
为不相关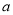 为正相关,
为正相关,  为不相关,
为不相关,  为负相关
为负相关 如图,四边形ABCD为矩形,DA⊥平面ABE,AE=EB=BC=2,BF⊥平面ACE于点F,且点F在CE上.
如图,四边形ABCD为矩形,DA⊥平面ABE,AE=EB=BC=2,BF⊥平面ACE于点F,且点F在CE上.



