题目内容
20.某校对数学、物理两科进行学业水平考前辅导,辅导后进行测试,按照成绩(满分均为100分)划分为合格(成绩大于或等于70分)和不合格(成绩小于70分).现随机抽取两科各100名学生的成绩统计如下:| 成绩(单位:分) | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
| 数学 | 8 | 12 | 40 | 32 | 8 |
| 物理 | 7 | 18 | 40 | 29 | 6 |
(2)设数学合格一人可以赢得4小时机器人操作时间,不合格一人则减少1小时机器人操作时间;物理合格一人可以赢得5小时机器人操作时间,不合格一人则减少2小时机器人操作时间.在(1)的前提下,
(i)记X为数学一人和物理一人共同赢得的机器人操作时间(单位:小时)总和,求随机变量X的分布列和数学期望;
(ii)随机抽取4名学生,求这四名学生物理考前辅导后进行测试所赢得的机器人操作时间不少于13小时的概率.
分析 (1)由等可能事件概率计算公式能求出数学合格率和物理合格率.
(2)(i)随机事件X的取值为9,4,2,-3,分别求出相应的概率,由此能求出X的分布列和EX.
(ii)设这4名学生物理辅导后测试合格人数为n(n=0,1,2,3,4),则由题意得:5n-2(4-n)≥13,由此能求出这四名学生物理考前辅导后进行测试所赢得的机器人操作时间不少于13小时的概率.
解答 解:(1)数学合格率${p}_{1}=\frac{40+32+8}{100}=\frac{4}{5}$,….1
物理合格率p2=$\frac{40+29+6}{100}$=$\frac{3}{4}$.…2
(2)(i)随机事件X的取值为9,4,2,-3,
P(X=9)=$\frac{4}{5}×\frac{3}{4}=\frac{3}{5}$,….3
P(X=4)=(1-$\frac{4}{5}$)×$\frac{3}{4}$=$\frac{3}{20}$,…4
P(X=2)=$\frac{4}{5}×(1-\frac{3}{4})$=$\frac{1}{5}$,…5
P(X=-3)=(1-$\frac{4}{5}$)×(1-$\frac{3}{4}$)=$\frac{1}{20}$,…6
X的分布列:
| X | 9 | 4 | 2 | -3 |
| P | $\frac{3}{5}$ | $\frac{3}{20}$ | $\frac{1}{5}$ | $\frac{1}{20}$ |
(ii)设这4名学生物理辅导后测试合格人数为n(n=0,1,2,3,4),
则由题意得:5n-2(4-n)≥13,解得n≥3,故n=3或n=4,…10
∴这四名学生物理考前辅导后进行测试所赢得的机器人操作时间不少于13小时的概率:
p=${C}_{4}^{3}(\frac{3}{4})^{3}(1-\frac{3}{4})+{C}_{4}^{4}(\frac{3}{4})^{4}$=$\frac{189}{256}$.…12
点评 本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,在历年高考中都是必考题型之一.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
12.对部分4G手机用户每日使用流量(单位:M)进行统计,得到如下记录:
将手机日使用的流量统计到各组的频率视为概率,并假设每天手机的日流量相互独立.
(Ⅰ)求某人在未来连续4天里,有连续3天的手机的日使用流量都不低于15M且另1天的手机日使用流量低于5M的概率;
(Ⅱ)用X表示某人在未来3天时间里手机日使用流量不低于15M的天数,求X的分布列和数学期望.
| 流量x | 0≤x<5 | 5≤x<10 | 10≤x<15 | 15≤x<20 | 20≤x<25 | x≥25 |
| 频率 | 0.05 | 0.25 | 0.30 | 0.25 | 0.15 | 0 |
(Ⅰ)求某人在未来连续4天里,有连续3天的手机的日使用流量都不低于15M且另1天的手机日使用流量低于5M的概率;
(Ⅱ)用X表示某人在未来3天时间里手机日使用流量不低于15M的天数,求X的分布列和数学期望.





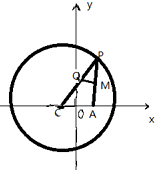 已知点C为圆(x+1)2+y2=8的圆心,P是圆上的动点,点Q在圆的半径CP上,且有点A(1,0)和AP上的点M,满足$\overrightarrow{MQ}$•$\overrightarrow{AP}$=0,$\overrightarrow{AP}$=2$\overrightarrow{AM}$.
已知点C为圆(x+1)2+y2=8的圆心,P是圆上的动点,点Q在圆的半径CP上,且有点A(1,0)和AP上的点M,满足$\overrightarrow{MQ}$•$\overrightarrow{AP}$=0,$\overrightarrow{AP}$=2$\overrightarrow{AM}$.