题目内容
二项式(x+1)8(x-1)展开式中x5的系数是( )
| A、-14 | B、14 |
| C、-28 | D、28 |
考点:二项式系数的性质
专题:二项式定理
分析:根据二项展开式为(
•x8+
•x7+…+
•x+
)(x-1),求得展开式中x5的系数.
| C | 0 8 |
| C | 1 8 |
| C | 7 8 |
| C | 8 8 |
解答:
解:二项式(x+1)8(x-1)=(
•x8+
•x7+…+
•x+
)(x-1),
故展开式中x5的系数是
-
=14,
故选:B.
| C | 0 8 |
| C | 1 8 |
| C | 7 8 |
| C | 8 8 |
故展开式中x5的系数是
| C | 4 8 |
| C | 3 8 |
故选:B.
点评:本题主要考查二项式定理的应用,二项式展开式的通项公式,求展开式中某项的系数,属于中档题.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
从集合{2,3,4,
,
}中取两个不同的数a,b,则logab>0的概率为( )
| 1 |
| 2 |
| 2 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
若复数Z=a2-1+(a-1)i(其中a∈R)为纯虚数,则复数
在复平面内对应的点位于( )
| 1+ai |
| 2+3i |
| A、第二或第三象限 |
| B、第三或第四象限 |
| C、第三象限 |
| D、第四象限 |
阅读程序框图,若输出的函数值在区间[0,4]上,则输入的实数x的取值范围是( )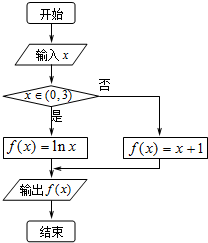

| A、{x∈R|-1≤x≤0或1≤x≤3} |
| B、{x∈R|-1≤x≤0或1≤x<3} |
| C、{x∈R|-1≤x≤0或1≤x≤e4} |
| D、{x∈R|-1≤x≤3} |
已知函数f(x)=
,若函数y=|f(x)|-k(x+e2)的零点恰有四个,则实数k的值为( )
|
| A、e | ||
B、
| ||
| C、e2 | ||
D、
|
已知函数f(x)=2x-1-log
x,则f(x)的零点的个数为( )
| 1 |
| 2 |
| A、0 | B、1 | C、2 | D、3 |