题目内容
已知△ABC中,a=4,b=4,∠A=30°,则∠B等于( )
| A、60°或120° |
| B、30°或150° |
| C、60° |
| D、30° |
考点:正弦定理
专题:解三角形
分析:直接利用正弦定理化简求解即可.
解答:
解:由题意在△ABC中,a=4,b=4,∠A=30°,
由正弦定理:
=
可得sinB=
=
=
.∴B=30°.
故选:D.
由正弦定理:
| a |
| sinA |
| b |
| sinB |
| bsinA |
| a |
4×
| ||
| 4 |
| 1 |
| 2 |
故选:D.
点评:本题考查正弦定理的应用,基本知识的考查.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
曲线y=
与直线y=x-1及x=4所围成的封闭图形的面积为( )
| 2 |
| x |
| A、2ln2 |
| B、2-ln2 |
| C、4-ln2 |
| D、4-2ln2 |
若a>b>0,c>d>0,则一定有( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
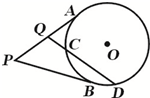 已知PA,PB分别为⊙O的两条切线,切点分别为A,B,过PA的中点Q作割线交⊙O于C,D两点,若QC=2,CD=3,则PB=
已知PA,PB分别为⊙O的两条切线,切点分别为A,B,过PA的中点Q作割线交⊙O于C,D两点,若QC=2,CD=3,则PB=