题目内容
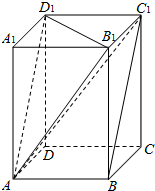 如图,正四棱柱ABCD-A1B1C1D1的底面边长为1,异面直线AD与BC1所成角的大小为60°,求:
如图,正四棱柱ABCD-A1B1C1D1的底面边长为1,异面直线AD与BC1所成角的大小为60°,求:(1)线段A1B1到底面ABCD的距离;
(2)三棱椎B1-ABC1的体积.
考点:棱柱、棱锥、棱台的体积,点、线、面间的距离计算
专题:空间位置关系与距离
分析:(1)由AD∥BC得CBC1=60°,由已知线段BB1的长为线段A1B1到底面ABCD的距离,由此能求出线段A1B1到底面ABCD的距离.
(2)由VB1-ABC1=VA-BB1C1,利用等积法能求出三棱椎的体积.
(2)由VB1-ABC1=VA-BB1C1,利用等积法能求出三棱椎的体积.
解答:
解:(1)∵AD∥BC,∴∠CBC1为异面直线AD与BC1所成角,
∴CBC1=60°,…(2分)
∵正四棱柱ABCD-A1B1C1D1中,
A1B1∥面ABCD,BB1⊥面ABCD,
∴线段BB1的长为线段A1B1到底面ABCD的距离,…(4分)
∵RT△BCC1中,BC=1,∠CBC1=60°,∴BB1=CC1=
,
线段A1,B1到底面ABCD的距离为
.…(6分)
(2)VB1-ABC1=VA-BB1C1…(8分)
=
×AB×S△BB1C1
=
×1×(
×1×
)…(10分)
=
.…(12分)
∴CBC1=60°,…(2分)
∵正四棱柱ABCD-A1B1C1D1中,
A1B1∥面ABCD,BB1⊥面ABCD,
∴线段BB1的长为线段A1B1到底面ABCD的距离,…(4分)
∵RT△BCC1中,BC=1,∠CBC1=60°,∴BB1=CC1=
| 3 |
线段A1,B1到底面ABCD的距离为
| 3 |
(2)VB1-ABC1=VA-BB1C1…(8分)
=
| 1 |
| 3 |
=
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
=
| ||
| 6 |
点评:本题考查线段到平面的距离的求法,考查三棱锥的体积的求法,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 目标测试系列答案
目标测试系列答案
相关题目
已知数列{an}的各项均为正数,Sn为其前n项的和,且对于任意的n∈N*,都有4Sn=(an+1)2.
(1)求a1,a2的值和数列{an}的通项公式;
(2)求数列bn=
的前n项和Tn.
(1)求a1,a2的值和数列{an}的通项公式;
(2)求数列bn=
| 1 |
| an•an+1 |
设F1、F2是双曲线C:
-
=1(a>0,b>0)的两个焦点,P是C上一点,若|PF1|+|PF2|=6a,且△PF1F2最小内角的大小为30°,则双曲线C的渐近线方程是( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||
B、x±
| ||
| C、x±2y=0 | ||
| D、2x±y=0 |