题目内容
19.设函数f(x)=log3(a+x)+log3(2-x)(a∈R)是偶函数.(1)若f(p)=1,求实数p的值;
(2)若存在m使得f(2m-1)<f(m)成立,试求实数m的取值范围.
分析 (1)根据函数f(x)是偶函数,f(-x)=f(x),求出a的值,写出f(x)的解析式,利用f(p)=1,解方程求出p的值;
(2)化简f(x),判断f(x)的单调性,把f(2m-1)<f(m)转化为等价的不等式组,求出解集即可.
解答 解:因为函数f(x)是偶函数,所以满足f(-x)=f(x);
即f(-x)=log3(a-x)+log3(2+x)=f(x)=log3(a+x)+log3(2-x),
所以(a-x)(2+x)=(a+x)(2-x),
解得a=2;
(1)f(x)=log3(2+x)+log3(2-x),
其定义域为(-2,2);
因为f(p)=1,所以log3(2+p)+log3(2-p)=1,
即4-p2=3,解得p=±1;
所以实数p的值为±1.
(2)因为$f(x)={log_3}(2+x)+{log_3}(2-x)={log_3}(4-{x^2})$,
所以函数f(x)在(-2,0]上单调递增,在[0,2)上单调递减;
因为f(2m-1)<f(m),所以f(|2m-1|)<f(|m|),
所以有$\left\{\begin{array}{l}|{2m-1}|>|m|\\-2<2m-1<2\\-2<m<2\end{array}\right.$,
解得$-\frac{1}{2}<m<\frac{1}{3}$或$1<m<\frac{3}{2}$;
所以满足条件的实数m的取值范围是$(-\frac{1}{2},\frac{1}{3})∪(1,\frac{3}{2})$.
点评 本题考查了函数的奇偶性与单调性问题,也考查了不等式的解法与应用问题,是综合性题目.

练习册系列答案
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
10.函数y=(5x-3)3的导数是( )
| A. | y'=3(5x-3)2 | B. | y'=15(5x-3)2 | C. | y'=9(5x-3)2 | D. | y'=12(5x-3)2 |
10.设三条不同的直线l1,l2,l3满足l1⊥l3,l2⊥l3,则l1与l2( )
| A. | 是异面直线 | B. | 是相交直线 | ||
| C. | 是平行直线 | D. | 可能相交,或相交,或异面直线 |
7.要得到函数$y=\frac{{\sqrt{2}}}{2}sinx+\frac{{\sqrt{2}}}{2}cosx+1$的图象,需要把函数y=sinx的图象( )
| A. | 向右平移$\frac{π}{4}$个单位,再向上平移1个单位 | |
| B. | 向左平移$\frac{π}{4}$个单位,再向上平移1个单位 | |
| C. | 向左平移$\frac{π}{4}$个单位,再向下平移1个单位 | |
| D. | 向右平移$\frac{π}{4}$个单位,再向下平移1个单位 |
4.已知sinα+cosα=-$\frac{1}{5}$,α∈(0,π),则tanα的值为( )
| A. | -$\frac{4}{3}$或-$\frac{3}{4}$ | B. | -$\frac{4}{3}$ | C. | -$\frac{3}{4}$ | D. | $\frac{3}{4}$ |
8.满足{1,2}?A⊆{1,2,3,4,5,6}的集合A的个数有( )个.
| A. | 13 | B. | 14 | C. | 15 | D. | 16 |
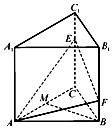 三棱柱ABC-A1B1C1的底面是边长为2的正三角形,侧棱A1A⊥底面ABC,点E,F分别是棱CC1,BB1上的点,点M是线段AC上的动点,EC=2FB=2.
三棱柱ABC-A1B1C1的底面是边长为2的正三角形,侧棱A1A⊥底面ABC,点E,F分别是棱CC1,BB1上的点,点M是线段AC上的动点,EC=2FB=2.