题目内容
11.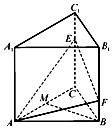 三棱柱ABC-A1B1C1的底面是边长为2的正三角形,侧棱A1A⊥底面ABC,点E,F分别是棱CC1,BB1上的点,点M是线段AC上的动点,EC=2FB=2.
三棱柱ABC-A1B1C1的底面是边长为2的正三角形,侧棱A1A⊥底面ABC,点E,F分别是棱CC1,BB1上的点,点M是线段AC上的动点,EC=2FB=2.(1)当点M在什么位置时,有BM∥平面AEF,并加以证明.
(2)求四棱锥A-BCEF的表面积.
分析 (1)M为AC中点;取AE的中点O,连接OF,OM;证明BM∥OF,即可证明BM∥平面AEF;
(2)分别计算四棱锥A-BCEF各个面的面积,求和即可.
解答 解:(1)M为AC中点;
证明如下:取AE的中点O,连接OF,OM;
∵O,M分别为AE,AC的中点,
∴OM∥CE,
∵BF∥CE,且EC=2FB=2,
∴OM∥FB∥CE,且OM=FB=$\frac{1}{2}CE$;
∴四边形OMBF为矩形,
故BM∥OF;
又BM?平面AEF,OF?平面AEF,
∴BM∥平面AEF;
(2)四棱锥A-BCEF的表面积为
S=S梯形BCEF+S△ABC+S△ABF+S△AEF+S△ACE
=$\frac{1}{2}$×(1+2)×2+$\frac{1}{2}$×22×sin$\frac{π}{3}$+$\frac{1}{2}$×2×1+$\frac{1}{2}$×2$\sqrt{2}$×$\sqrt{5-2}$+$\frac{1}{2}$×2×2
=6+$\sqrt{3}$+$\sqrt{6}$.
点评 本题考查了空间中的平行与垂直关系的应用问题,也考查了几何体表面积的计算问题,是综合题.

练习册系列答案
相关题目
2.已知定义在R上的可导函数f(x)的导函数为f'(x),满足f'(x)<f(x),且f(x+2)=f(-x+2),f(4)=1,则不等式f(x)<ex的解集为( )
| A. | (-∞,e4) | B. | (e4,+∞) | C. | (-∞,0) | D. | (0,+∞) |
6.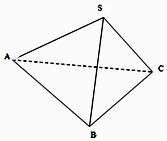 如图,已知三棱锥S-ABC中,SA=SB=CA=CB=$\sqrt{3}$,AB=2,SC=$\sqrt{2}$,则二面角S-AB-C的平面角的大小为( )
如图,已知三棱锥S-ABC中,SA=SB=CA=CB=$\sqrt{3}$,AB=2,SC=$\sqrt{2}$,则二面角S-AB-C的平面角的大小为( )
 如图,已知三棱锥S-ABC中,SA=SB=CA=CB=$\sqrt{3}$,AB=2,SC=$\sqrt{2}$,则二面角S-AB-C的平面角的大小为( )
如图,已知三棱锥S-ABC中,SA=SB=CA=CB=$\sqrt{3}$,AB=2,SC=$\sqrt{2}$,则二面角S-AB-C的平面角的大小为( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
20.集合{-2,1}等于( )
| A. | {(x-1)(x+2)=0} | B. | {y|y=x+1,x∈Z} | C. | {x|(x+1)(x-2)=0} | D. | {x|(x-1)(x+2)=0} |
 如图,在四棱锥P-ABCD中,O为AC与BD的交点,AB⊥平面PAD,△PAD是正三角形,DC∥AB,DA=DC=2AB=2a.
如图,在四棱锥P-ABCD中,O为AC与BD的交点,AB⊥平面PAD,△PAD是正三角形,DC∥AB,DA=DC=2AB=2a.