题目内容
在平面直角坐标系中,以坐标原点为极点,x轴的非负半轴为极轴建立极坐标系.已知直线l的参数方程为
(t为参数),圆C的极坐标方程为ρ=2
cos(θ-
).若圆C关于直线l对称,则a的值为 .
|
| 2 |
| π |
| 4 |
考点:参数方程化成普通方程
专题:坐标系和参数方程
分析:直线l的参数方程为
(t为参数),消去参数t可得x+ay+a-5=0.圆C的极坐标方程为ρ=2
cos(θ-
),展开并把
代入即可得出直角坐标方程.由于圆C关于直线l对称,可得圆心C在直线l上.
|
| 2 |
| π |
| 4 |
|
解答:
解:直线l的参数方程为
(t为参数),消去参数t可得x+ay+a-5=0.
圆C的极坐标方程为ρ=2
cos(θ-
)展开化为ρ2=2
(
ρcosθ+
ρsinθ).
把
代入可得x2+y2=2x+2y.
化为(x-1)2+(y-1)2=2.圆心C(1,1).
∵圆C关于直线l对称,
∴圆心C在直线l上,
∴1+a+a-5=0,
解得a=2.
则a的值为 2.
故答案为:2.
|
圆C的极坐标方程为ρ=2
| 2 |
| π |
| 4 |
| 2 |
| ||
| 2 |
| ||
| 2 |
把
|
化为(x-1)2+(y-1)2=2.圆心C(1,1).
∵圆C关于直线l对称,
∴圆心C在直线l上,
∴1+a+a-5=0,
解得a=2.
则a的值为 2.
故答案为:2.
点评:本题考查了直线的参数方程化为普通方程、极坐标方程化为直角坐标方程、圆的对称性,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
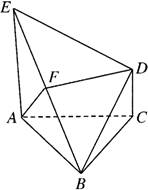 已知:△ABC是正三角形,EA、CD垂直平面ABC,且EA=AB=2,DC=1,F是BE中点.求证:(1)FD∥平面ABC;
已知:△ABC是正三角形,EA、CD垂直平面ABC,且EA=AB=2,DC=1,F是BE中点.求证:(1)FD∥平面ABC;