题目内容
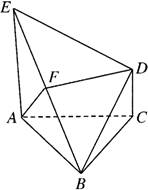 已知:△ABC是正三角形,EA、CD垂直平面ABC,且EA=AB=2,DC=1,F是BE中点.求证:(1)FD∥平面ABC;
已知:△ABC是正三角形,EA、CD垂直平面ABC,且EA=AB=2,DC=1,F是BE中点.求证:(1)FD∥平面ABC;(2)AF⊥平面BDE.
考点:直线与平面垂直的判定,直线与平面平行的判定
专题:空间位置关系与距离
分析:(1)过F作FO∥EA,只要证明FD∥CO即可;
(2)因为AE⊥平面ABC,AE?平面AEB,得到平面AEB⊥平面ABC,再由面面垂直的性质得到OC⊥平面ABE,进一步得到AF⊥OC,由线面垂直的判定定理可证.
(2)因为AE⊥平面ABC,AE?平面AEB,得到平面AEB⊥平面ABC,再由面面垂直的性质得到OC⊥平面ABE,进一步得到AF⊥OC,由线面垂直的判定定理可证.
解答:
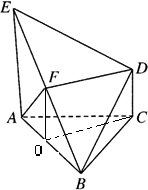 证明:(1)过F作FO∥EA,因为F是EB的中点,所以O是AB的中点,所以FO∥CD,FO=CD,
证明:(1)过F作FO∥EA,因为F是EB的中点,所以O是AB的中点,所以FO∥CD,FO=CD,
所以四边形FOCD是平行四边形,所以FD∥CO,又FD?平面ABC,CO?平面ABC,
所以FD∥平面ABC;
(2)∵AE⊥平面ABC,AE?平面AEB,
∴平面AEB⊥平面ABC,
又平面AEB∩平面ABC=AB,OC⊥AB,
∴OC⊥平面ABE,AF?平面ABE,
∴AF⊥OC,DF∥OC
∴AF⊥DF又AF⊥BE,
∴AF⊥平面BDE.
 证明:(1)过F作FO∥EA,因为F是EB的中点,所以O是AB的中点,所以FO∥CD,FO=CD,
证明:(1)过F作FO∥EA,因为F是EB的中点,所以O是AB的中点,所以FO∥CD,FO=CD,所以四边形FOCD是平行四边形,所以FD∥CO,又FD?平面ABC,CO?平面ABC,
所以FD∥平面ABC;
(2)∵AE⊥平面ABC,AE?平面AEB,
∴平面AEB⊥平面ABC,
又平面AEB∩平面ABC=AB,OC⊥AB,
∴OC⊥平面ABE,AF?平面ABE,
∴AF⊥OC,DF∥OC
∴AF⊥DF又AF⊥BE,
∴AF⊥平面BDE.
点评:本题考查了线面平行的判定和线面垂直的判定,关键是熟练相关的判定定理和性质定理,将线面关系转化为线线关系解答.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目
轮船A和轮船B在某日中午12时离开海港C,两艘轮船的航行方向之间的夹角为120°,轮船A的航行速度是25/h,轮船B的航行速度是15n mile/h,则该日下午2时A、B两船之间的距离是( )
| A、35 n mile | ||
B、5
| ||
| C、70 n mile | ||
D、10
|
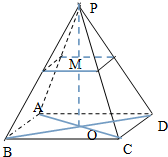 如图,已知四棱锥P-ABCD的底边长与侧棱的长度都是4,ABCD是正方形.
如图,已知四棱锥P-ABCD的底边长与侧棱的长度都是4,ABCD是正方形.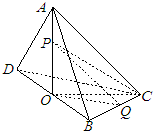 如图,已知BC=DC=AB=AD=
如图,已知BC=DC=AB=AD= 如图,在底面为平行四边形的四棱锥P-ABCD中,AB⊥AC,PA⊥平面ABCD,且PA=2AB=2,E是线段PD上的点.
如图,在底面为平行四边形的四棱锥P-ABCD中,AB⊥AC,PA⊥平面ABCD,且PA=2AB=2,E是线段PD上的点.