题目内容
20.已知复数z满足z$\overline{z}$+2i$\overline{z}$=3+ai(a∈R),且z对应的点在第二象限,求实数a的取值范围.分析 利用已知条件求出复数z,列出不等式组,求解即可.
解答 解:复数z满足z$\overline{z}$+2i$\overline{z}$=3+ai(a∈R),
可设z=m+ni.z对应的点在第二象限,可知m<0,n>0.
则m2+n2+2i(m-ni)=3+ai,
$\left\{\begin{array}{l}{{m}^{2}+{n}^{2}+2n=3}\\{2m=a}\end{array}$,
解得:m=$\frac{a}{2}$,n=$\frac{-2+\sqrt{4-4(-3+\frac{{a}^{2}}{4})}}{2}$>0,
解得:-2$\sqrt{3}$<a<0.
点评 本题考查复数的基本概念,复数方程的求法,考查计算能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10.执行如图所示的程序框图,输出的n为( )


| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
11.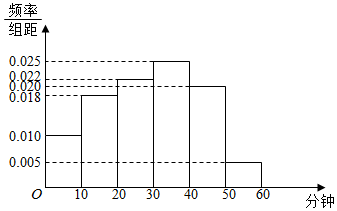 某中学为研究学生的身体素质与课外体育锻炼时间的关系,对该校200名学生的课外体育锻炼平均每天运动的时间(单位:分钟)进行调查,将收集到的数据分成[0,10),[10,20),[20,30),[30,40),[40,50),[50,60)六组,并作出频率分布直方图(如图).将日均课外体育锻炼时间不低于40分钟的学生评价为“课外体育达标”.
某中学为研究学生的身体素质与课外体育锻炼时间的关系,对该校200名学生的课外体育锻炼平均每天运动的时间(单位:分钟)进行调查,将收集到的数据分成[0,10),[10,20),[20,30),[30,40),[40,50),[50,60)六组,并作出频率分布直方图(如图).将日均课外体育锻炼时间不低于40分钟的学生评价为“课外体育达标”.
(1)请根据直方图中的数据填写下面的2×2列联表,并通过计算判断是否能在犯错误的概率不超过0.01的前提下认为“课外体育达标”与性别有关?
(2)现从课外体育达标学生中按分层抽样抽取5人,再从这5名学生中随机抽取2人参加体育知识问卷调查,求抽取的这2人课外锻炼时间都在[40,50)内的概率.
附参考公式与数据:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
 某中学为研究学生的身体素质与课外体育锻炼时间的关系,对该校200名学生的课外体育锻炼平均每天运动的时间(单位:分钟)进行调查,将收集到的数据分成[0,10),[10,20),[20,30),[30,40),[40,50),[50,60)六组,并作出频率分布直方图(如图).将日均课外体育锻炼时间不低于40分钟的学生评价为“课外体育达标”.
某中学为研究学生的身体素质与课外体育锻炼时间的关系,对该校200名学生的课外体育锻炼平均每天运动的时间(单位:分钟)进行调查,将收集到的数据分成[0,10),[10,20),[20,30),[30,40),[40,50),[50,60)六组,并作出频率分布直方图(如图).将日均课外体育锻炼时间不低于40分钟的学生评价为“课外体育达标”.(1)请根据直方图中的数据填写下面的2×2列联表,并通过计算判断是否能在犯错误的概率不超过0.01的前提下认为“课外体育达标”与性别有关?
| 课外体育不达标 | 课外体育达标 | 合计 | |
| 男 | 60 | 30 | 90 |
| 女 | 90 | 20 | 110 |
| 合计 | 150 | 50 | 200 |
附参考公式与数据:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
| P(K2≥k0) | 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
| k0 | 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
12.若a>b>1,0<c<1,则( )
| A. | ac<bc | B. | abc<bac | C. | alogbc<blogac | D. | logac<logbc |