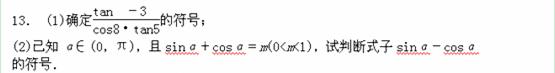题目内容
设函数f(x)=x-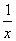 -aln x(a∈R).
-aln x(a∈R).
(1)讨论f(x)的单调性;
(2)若f(x)有两个极值点x1和x2,记过点A(x1,f(x1)),B(x2,f(x2))的直线的斜率为k.问:是否存在a,使得k=2-a?若存在,求出a的值;若不存在,请说明理由.
思路分析 先求导,通分后发现f′(x)的符号与a有关,应对a进行分类,依据方程的判别式来分类.
解析 (1)f(x)的定义域为(0,+∞).
f′(x)=1+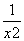 -
-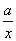 =
=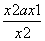 .
.
令g(x)=x2-ax+1,其判别式Δ=a2-4.
①当|a|≤2时,Δ≤0,f′(x)≥0.故f(x)在(0,+∞)上单调递增.
②当a<-2时,Δ>0,g(x)=0的两根都小于0.在(0,+∞)上,f′(x)>0.故f(x)在(0,+∞)上单调递增.
③当a>2时,Δ>0,g(x)=0的两根为x1=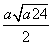 ,
,
x2=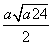 .
.
当0<x<x1时,f′(x)>0,当x1<x<x2时,f′(x)<0;
当x>x2时,f′(x)>0.故f(x)分别在(0,x1),(x2,+∞)上单调递增,在(x1,x2)上单调递减.
(2)由(1)知,a>2.
因为f(x1)-f(x2)=(x1-x2)+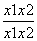 -a(ln x1-ln x2),所以,k=
-a(ln x1-ln x2),所以,k=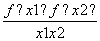 =1+
=1+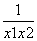 -a·
-a·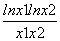 .
.
又由(1)知,x1x2=1,于是k=2-a·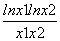 .
.
若存在a,使得k=2-a,则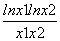 =1.
=1.
即ln x1-ln x2=x1-x2.
由x1x2=1得x2-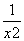 -2ln x2=0(x2>1).(*)
-2ln x2=0(x2>1).(*)
再由(1)知,函数h(t)=t-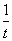 -2ln t在(0,+∞)上单调递增,而x2>1,所以x2-
-2ln t在(0,+∞)上单调递增,而x2>1,所以x2-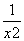 -2ln x2>1-
-2ln x2>1-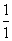 -2 ln 1=0.这与(*)式矛盾.
-2 ln 1=0.这与(*)式矛盾.
故不存在a,使得k=2-a.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
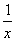 的单调增区间为( ).
的单调增区间为( ).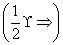

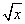 ,直线y=x-2及y轴所围成的图形的面积为
,直线y=x-2及y轴所围成的图形的面积为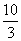 B.4
B.4  D.6
D.6