题目内容
16.已知函数f(x)=lnx.(1)求f(x)在点(1,f(1))处的切线;
(2)若?x∈[1,+∞),f(x)≤m(${x-\frac{1}{x}}$)恒成立,求实数m的取值范围;
(3)求证:ln(2n+1)<$\sum_{k=1}^n{\frac{4k}{{4{k^2}-1}}},({n∈{N_+}})$.
分析 (1)求出函数导数.求出切线的斜率,切点坐标,然后求解切线方程.
(2)设$g(x)=lnx-m({x-\frac{1}{x}})$,求出导函数,通过①若m≤0,②$m≥\frac{1}{2}$时,当$0<m<\frac{1}{2}$时,判断函数的单调性求出函数的最值,推出结果即可.
(3)由(2)知,当x>1时,$m=\frac{1}{2}$时,$lnx<\frac{1}{2}({x-\frac{1}{x}})$成立,不妨令$x=\frac{2k+1}{2k-1},k∈{N^*}$,通过证明$ln\frac{2k+1}{2k-1}<\frac{1}{2}({\frac{2k+1}{2k-1}-\frac{2k-1}{2k+1}})=\frac{4k}{{4{k^2}-1}}$,然后证明结果.
解答 解:(1)函数f(x)=lnx.可得f′(x)=$\frac{1}{x}$,f′(1)=1,又f(1)=0.
f(x)在点(1,0)处的切线:y=1(x-1).
即:y=x-1.
(2)$?x∈({1,+∞}),lnx≤m({x-\frac{1}{x}})$恒成立,设$g(x)=lnx-m({x-\frac{1}{x}})$,即$?x∈({1,+∞}),g(x)≤0,g'(x)=\frac{1}{x}-m({1+\frac{1}{x^2}})=\frac{{-m{x^2}+x-m}}{x^2}$.
①若m≤0,g'(x)>0,g(x)≥g(1)=0,这与题设g(x)≤0矛盾.
②若m>0方程-mx2+x-m=0的判别式△=1-4m2,
当△≤0,即$m≥\frac{1}{2}$时,g'(x)≤0,∴g(x)在(0,+∞)上单调递减,∴g(x)≤g(1)=0,即不等式成立.
当$0<m<\frac{1}{2}$时,方程-mx2+x-m=0,其根${x_1}=\frac{{1-\sqrt{1-4{m^2}}}}{2m}>0,{x_2}=\frac{{1+\sqrt{1-4{m^2}}}}{2m}>1$,
当x∈(1,x2)g'(x)>0,g(x)单调递增,g(x)>g(1)=0,与题设矛盾.综上所述,$m≥\frac{1}{2}$.
(3)由(2)知,当x>1时,$m=\frac{1}{2}$时,$lnx<\frac{1}{2}({x-\frac{1}{x}})$成立,不妨令$x=\frac{2k+1}{2k-1},k∈{N^*}$∴$ln\frac{2k+1}{2k-1}<\frac{1}{2}({\frac{2k+1}{2k-1}-\frac{2k-1}{2k+1}})=\frac{4k}{{4{k^2}-1}}$,$\sum_{k=1}^n{ln\frac{2k+1}{2k-1}}<\sum_{k=1}^n{\frac{4k}{{4{k^2}-1}}},({n∈{N_+}})$,
即$ln({2n+1})<\sum_{k=1}^n{\frac{4k}{{4{k^2}-1}}},({n∈{N_+}})$.
点评 本题考查函数的导数的应用,函数的最值,构造法以及转化思想的应用,考查计算能力.

| A. | $-\sqrt{a}$ | B. | $-\sqrt{-a}$ | C. | $\sqrt{-a}$ | D. | $\sqrt{a}$ |
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 既非充分又非必要条件 |
| A. | a<1或a>3 | B. | a>3 | C. | a<1 | D. | 1<a<3 |
| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 60 | 50 | 70 |
(2)据此估计广告费用为12万元时的销售额约为多少?
参考公式:$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$,$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$.
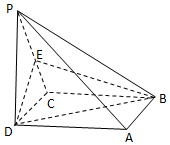 如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,